Data-Aware Random Feature Kernel for Transformers

Transformers excel across domains, yet their quadratic attention complexity poses a barrier to scaling. Random-feature attention, as in Performers, can reduce this cost to linear in the sequence length by approximating the softmax kernel with positive random features drawn from an isotropic distribution. In pretrained models, however, queries and keys are typically anisotropic. This induces high Monte Carlo variance in isotropic sampling schemes unless one retrains the model or uses a large feature budget. Importance sampling can address this by adapting the sampling distribution to the input geometry, but complex data-dependent proposal distributions are often intractable. We show that by data aligning the softmax kernel, we obtain an attention mechanism which can both admit a tractable minimal-variance proposal distribution for importance sampling, and exhibits better training stability. Motivated by this finding, we introduce DARKFormer, a Data-Aware Random-feature Kernel transformer that features a data-aligned kernel geometry. DARKFormer learns the random-projection covariance, efficiently realizing an importance-sampled positive random-feature estimator for its data-aligned kernel. Empirically, DARKFormer narrows the performance gap with exact softmax attention, particularly in finetuning regimes where pretrained representations are anisotropic. By combining random-feature efficiency with data-aware kernels, DARKFormer advances kernel-based attention in resource-constrained settings.

All Random Features Representations are Equivalent

Random features are an important technique that make it possible to rewrite positive-definite kernels as infinite-dimensional dot products. Over time, increasingly elaborate random feature representations have been developed in pursuit of finite approximations with ever lower error. We resolve this arms race by deriving an optimal sampling policy, and show that under this policy all random features representations have the same approximation error. This establishes a lower bound that holds across all random feature representations, and shows that we are free to choose whatever representation we please, provided we sample optimally.

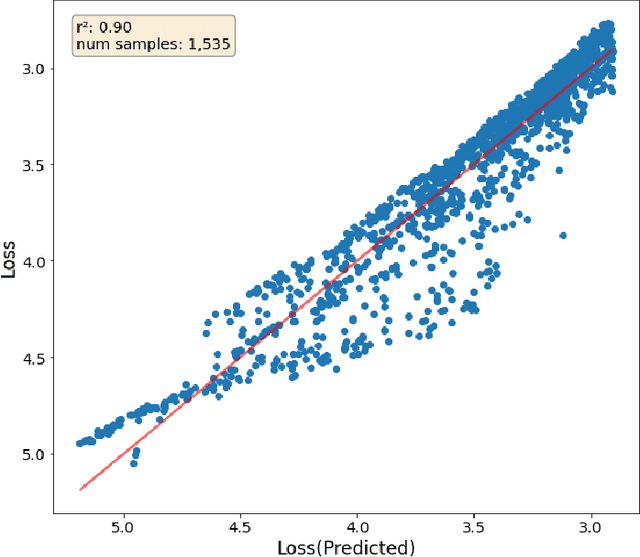
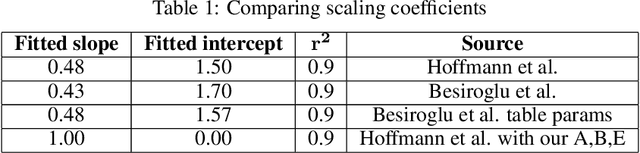
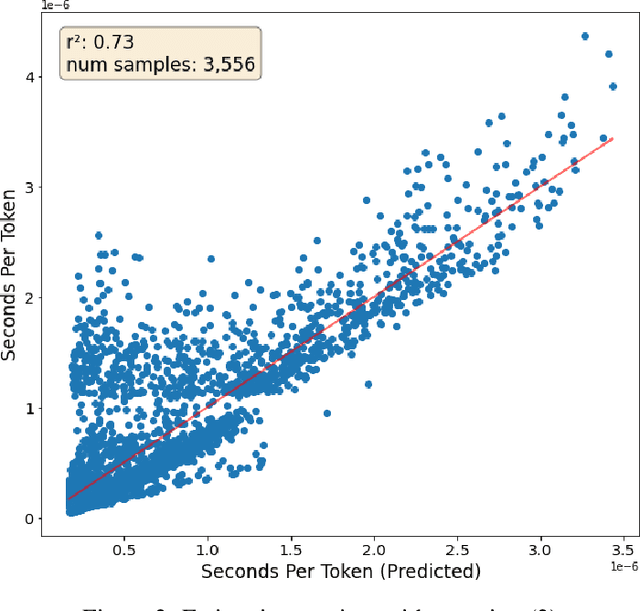
Time Matters: Scaling Laws for Any Budget

A primary cost driver for training large models is wall-clock training time. We show that popular time estimates based on FLOPs are poor estimates, and construct a more accurate proxy based on memory copies. We show that with some simple accounting, we can estimate the training speed of a transformer model from its hyperparameters. Combined with a scaling law curve like Chinchilla, this lets us estimate the final loss of the model. We fit our estimate to real data with a linear regression, and apply the result to rewrite Chinchilla in terms of a model's estimated training time as opposed to the amount of training data. This gives an expression for the loss in terms of the model's hyperparameters alone. We show that this expression is accurate across a wide range of model hyperparameter values, enabling us to analytically make architectural decisions and train models more efficiently.

Infinite Width Models That Work: Why Feature Learning Doesn't Matter as Much as You Think

Common infinite-width architectures such as Neural Tangent Kernels (NTKs) have historically shown weak performance compared to finite models. This has been attributed to the absence of feature learning. We show that this is not the case. In fact, we show that infinite width NTK models are able to access richer features than finite models by selecting relevant subfeatures from their (infinite) feature vector. In fact, we show experimentally that NTKs under-perform traditional finite models even when feature learning is artificially disabled. Instead, weak performance is due to the fact that existing constructions depend on weak optimizers like SGD. We provide an infinite width limit based on ADAM-like learning dynamics and demonstrate empirically that the resulting models erase this performance gap.