Luis F. Miranda
Solving the Exponential Growth of Symbolic Regression Trees in Geometric Semantic Genetic Programming
Apr 18, 2018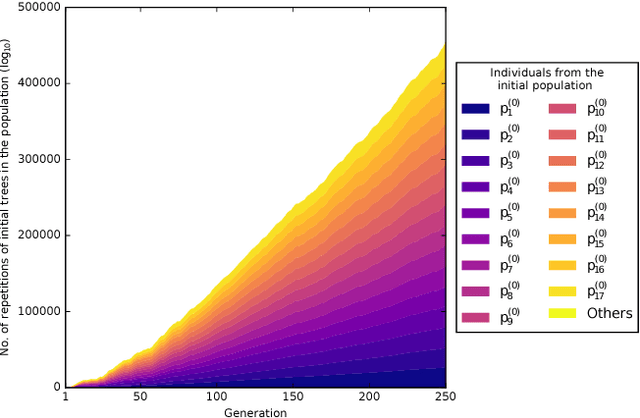
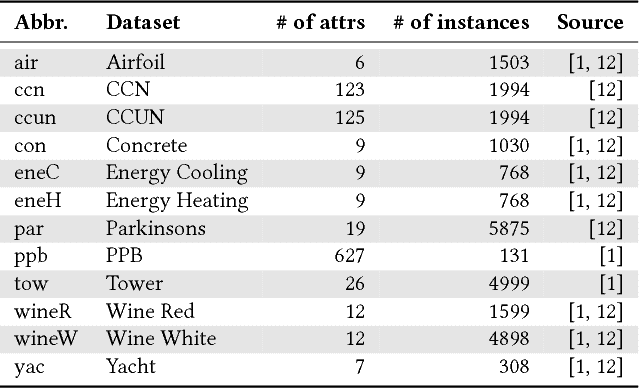
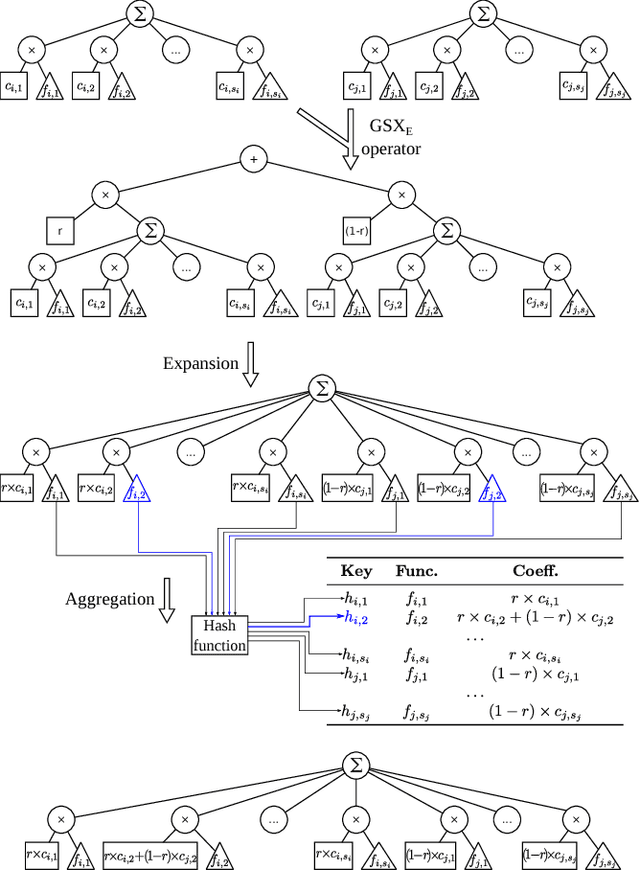
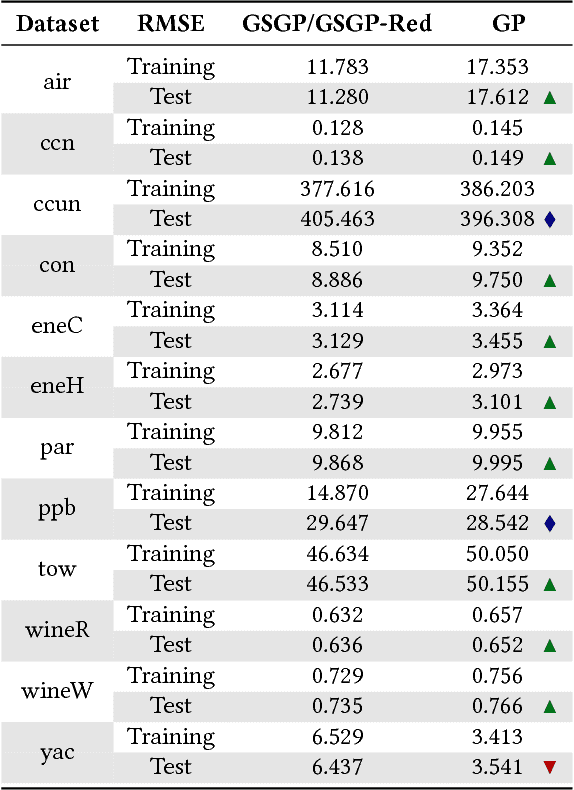
Abstract:Advances in Geometric Semantic Genetic Programming (GSGP) have shown that this variant of Genetic Programming (GP) reaches better results than its predecessor for supervised machine learning problems, particularly in the task of symbolic regression. However, by construction, the geometric semantic crossover operator generates individuals that grow exponentially with the number of generations, resulting in solutions with limited use. This paper presents a new method for individual simplification named GSGP with Reduced trees (GSGP-Red). GSGP-Red works by expanding the functions generated by the geometric semantic operators. The resulting expanded function is guaranteed to be a linear combination that, in a second step, has its repeated structures and respective coefficients aggregated. Experiments in 12 real-world datasets show that it is not only possible to create smaller and completely equivalent individuals in competitive computational time, but also to reduce the number of nodes composing them by 58 orders of magnitude, on average.
How Noisy Data Affects Geometric Semantic Genetic Programming
Jul 04, 2017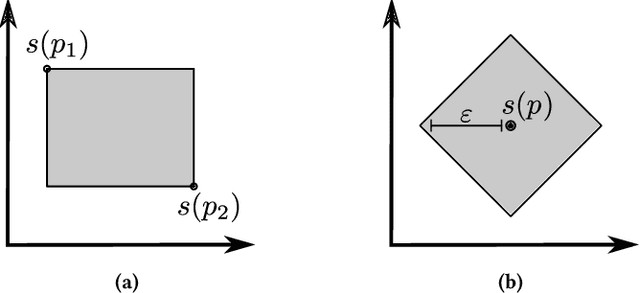
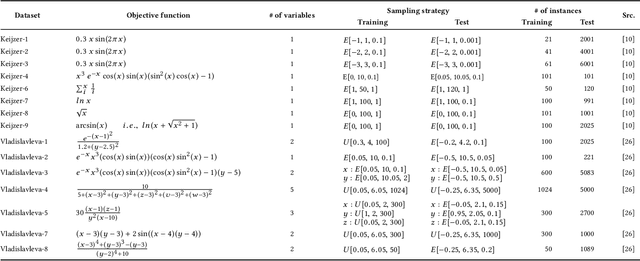

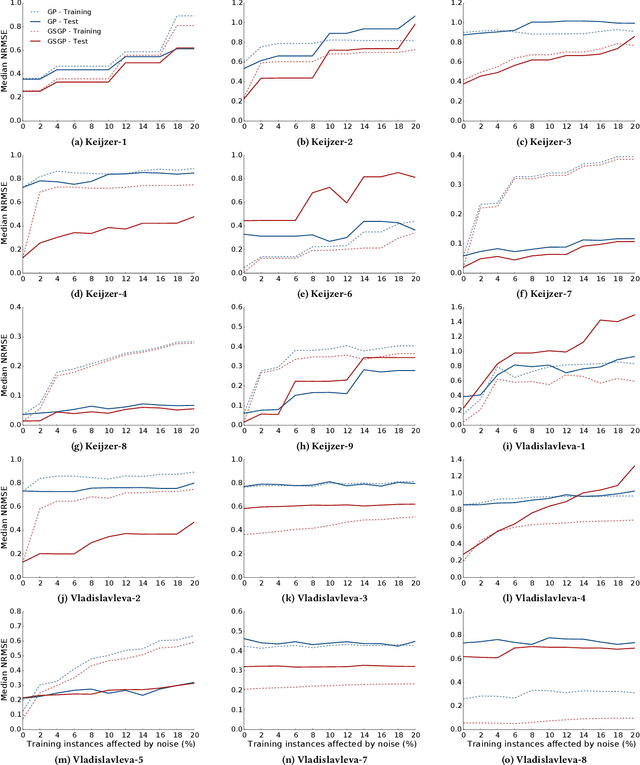
Abstract:Noise is a consequence of acquiring and pre-processing data from the environment, and shows fluctuations from different sources---e.g., from sensors, signal processing technology or even human error. As a machine learning technique, Genetic Programming (GP) is not immune to this problem, which the field has frequently addressed. Recently, Geometric Semantic Genetic Programming (GSGP), a semantic-aware branch of GP, has shown robustness and high generalization capability. Researchers believe these characteristics may be associated with a lower sensibility to noisy data. However, there is no systematic study on this matter. This paper performs a deep analysis of the GSGP performance over the presence of noise. Using 15 synthetic datasets where noise can be controlled, we added different ratios of noise to the data and compared the results obtained with those of a canonical GP. The results show that, as we increase the percentage of noisy instances, the generalization performance degradation is more pronounced in GSGP than GP. However, in general, GSGP is more robust to noise than GP in the presence of up to 10% of noise, and presents no statistical difference for values higher than that in the test bed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge