Felipe Casadei
Solving the Exponential Growth of Symbolic Regression Trees in Geometric Semantic Genetic Programming
Apr 18, 2018
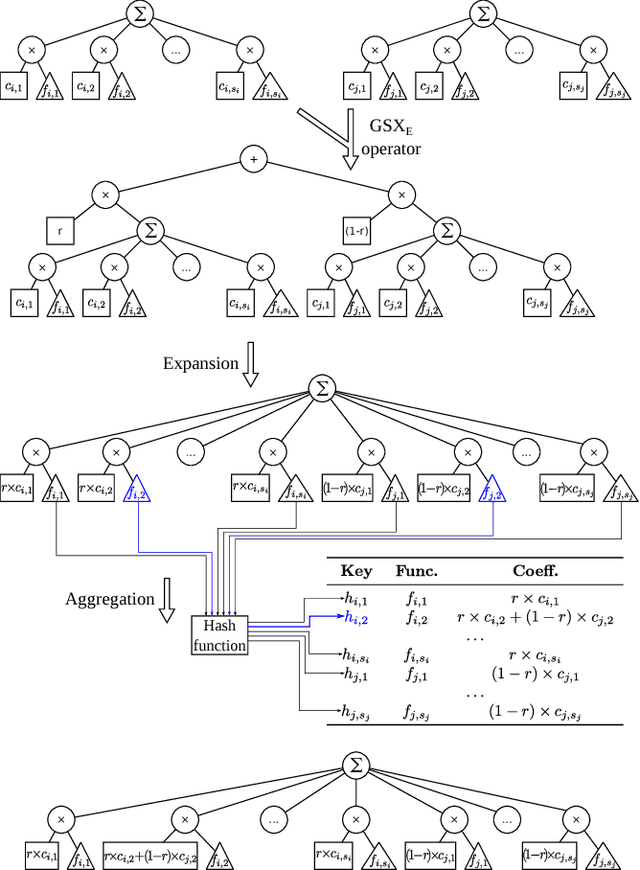
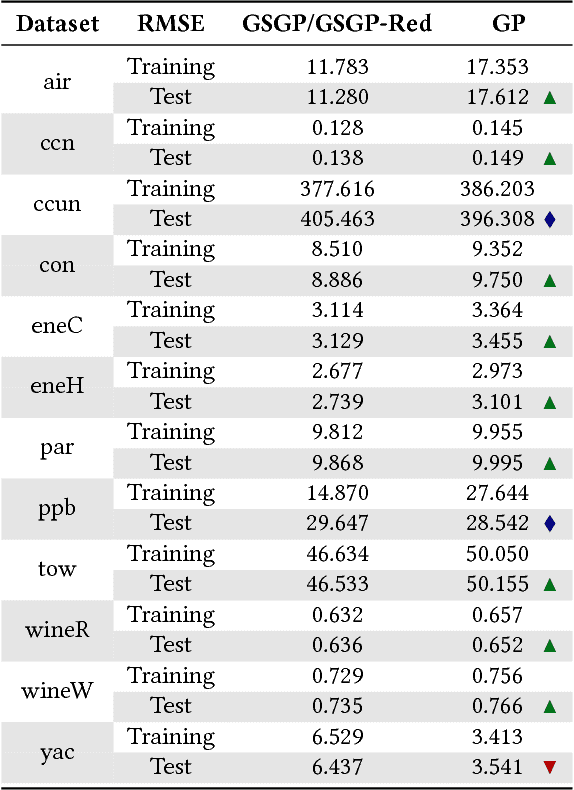
Abstract:Advances in Geometric Semantic Genetic Programming (GSGP) have shown that this variant of Genetic Programming (GP) reaches better results than its predecessor for supervised machine learning problems, particularly in the task of symbolic regression. However, by construction, the geometric semantic crossover operator generates individuals that grow exponentially with the number of generations, resulting in solutions with limited use. This paper presents a new method for individual simplification named GSGP with Reduced trees (GSGP-Red). GSGP-Red works by expanding the functions generated by the geometric semantic operators. The resulting expanded function is guaranteed to be a linear combination that, in a second step, has its repeated structures and respective coefficients aggregated. Experiments in 12 real-world datasets show that it is not only possible to create smaller and completely equivalent individuals in competitive computational time, but also to reduce the number of nodes composing them by 58 orders of magnitude, on average.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge