Lucas Pagliosa
Ensuring Learning Guarantees on Concept Drift Detection with Statistical Learning Theory
Jun 24, 2020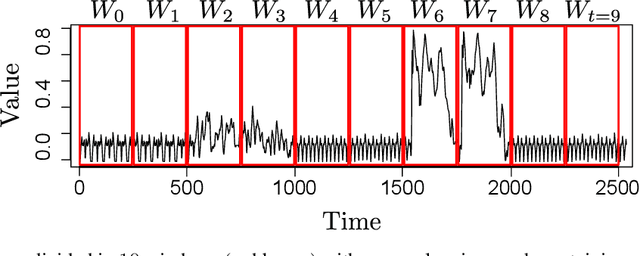


Abstract:Concept Drift (CD) detection intends to continuously identify changes in data stream behaviors, supporting researchers in the study and modeling of real-world phenomena. Motivated by the lack of learning guarantees in current CD algorithms, we decided to take advantage of the Statistical Learning Theory (SLT) to formalize the necessary requirements to ensure probabilistic learning bounds, so drifts would refer to actual changes in data rather than by chance. As discussed along this paper, a set of mathematical assumptions must be held in order to rely on SLT bounds, which are especially controversial in CD scenarios. Based on this issue, we propose a methodology to address those assumptions in CD scenarios and therefore ensure learning guarantees. Complementary, we assessed a set of relevant and known CD algorithms from the literature in light of our methodology. As main contribution, we expect this work to support researchers while designing and evaluating CD algorithms on different domains.
Supporting Optimal Phase Space Reconstructions Using Neural Network Architecture for Time Series Modeling
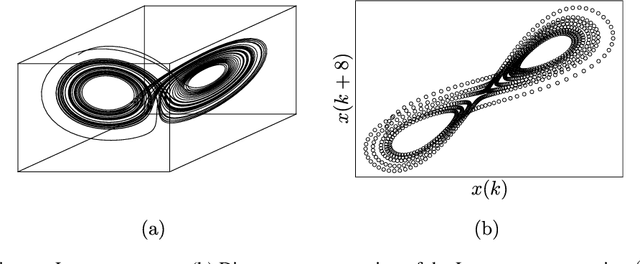
Jun 19, 2020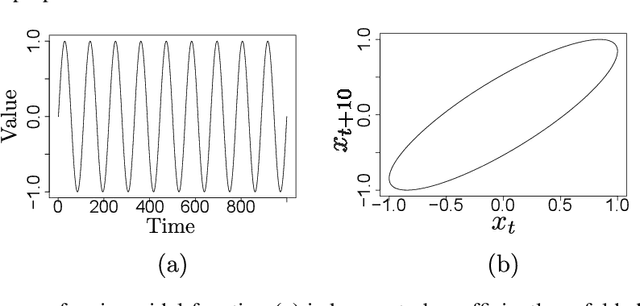
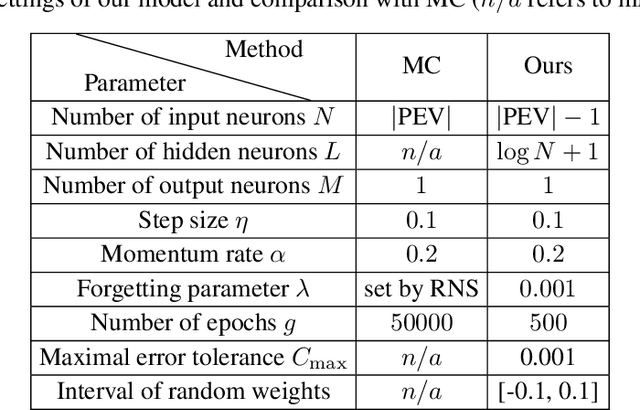
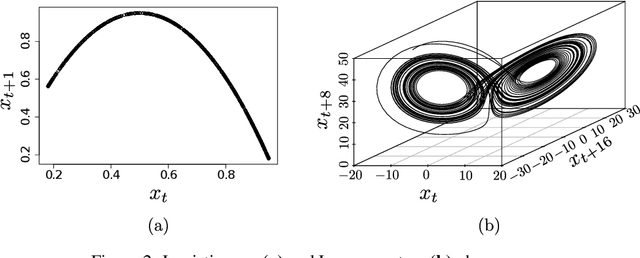
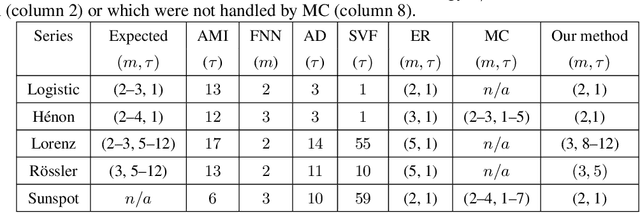
Abstract:The reconstruction of phase spaces is an essential step to analyze time series according to Dynamical System concepts. A regression performed on such spaces unveils the relationships among system states from which we can derive their generating rules, that is, the most probable set of functions responsible for generating observations along time. In this sense, most approaches rely on Takens' embedding theorem to unfold the phase space, which requires the embedding dimension and the time delay. Moreover, although several methods have been proposed to empirically estimate those parameters, they still face limitations due to their lack of consistency and robustness, which has motivated this paper. As an alternative, we here propose an artificial neural network with a forgetting mechanism to implicitly learn the phase spaces properties, whatever they are. Such network trains on forecasting errors and, after converging, its architecture is used to estimate the embedding parameters. Experimental results confirm that our approach is either as competitive as or better than most state-of-the-art strategies while revealing the temporal relationship among time-series observations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge