Lucas N. Egidio
Learning the Step-size Policy for the Limited-Memory Broyden-Fletcher-Goldfarb-Shanno Algorithm
Oct 03, 2020
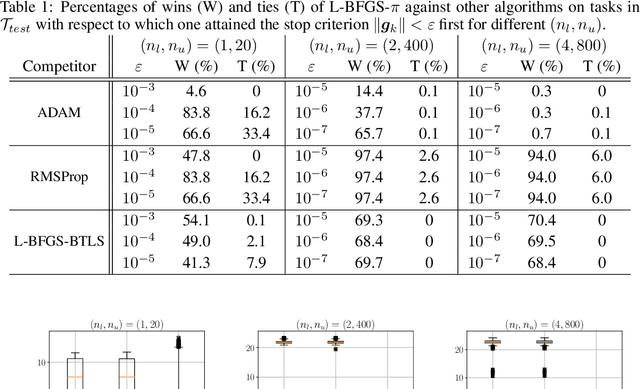
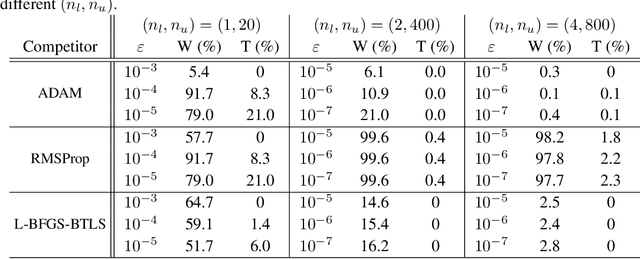
Abstract:We consider the problem of how to learn a step-size policy for the Limited-Memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) algorithm. This is a limited computational memory quasi-Newton method widely used for deterministic unconstrained optimization but currently avoided in large-scale problems for requiring step sizes to be provided at each iteration. Existing methodologies for the step size selection for L-BFGS use heuristic tuning of design parameters and massive re-evaluations of the objective function and gradient to find appropriate step-lengths. We propose a neural network architecture with local information of the current iterate as the input. The step-length policy is learned from data of similar optimization problems, avoids additional evaluations of the objective function, and guarantees that the output step remains inside a pre-defined interval. The corresponding training procedure is formulated as a stochastic optimization problem using the backpropagation through time algorithm. The performance of the proposed method is evaluated on the MNIST database for handwritten digits. The results show that the proposed algorithm outperforms heuristically tuned optimizers such as ADAM and RMSprop in terms of computational time. It performs comparably to more computationally demanding L-BFGS with backtracking line search. The numerical results also show that the learned policy generalizes better to high-dimensional problems as compared to ADAM and RMSprop, highlighting its potential use in large-scale optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge