Optimization of Iterative Blind Detection based on Expectation Maximization and Belief Propagation

We study iterative blind symbol detection for block-fading linear inter-symbol interference channels. Based on the factor graph framework, we design a joint channel estimation and detection scheme that combines the expectation maximization (EM) algorithm and the ubiquitous belief propagation (BP) algorithm. Interweaving the iterations of both schemes significantly reduces the EM algorithm's computational burden while retaining its excellent performance. To this end, we apply simple yet effective model-based learning methods to find a suitable parameter update schedule by introducing momentum in both the EM parameter updates as well as in the BP message passing. Numerical simulations verify that the proposed method can learn efficient schedules that generalize well and even outperform coherent BP detection in high signal-to-noise scenarios.

Fast and Robust Expectation Propagation MIMO Detection via Preconditioned Conjugated Gradient

We study the expectation propagation (EP) algorithm for symbol detection in massive multiple-input multiple-output (MIMO) systems. The EP detector shows excellent performance but suffers from a high computational complexity due to the matrix inversion, required in each EP iteration to perform marginal inference on a Gaussian system. We propose an inversion-free variant of the EP algorithm by treating inference on the mean and variance as two separate and simpler subtasks: We study the preconditioned conjugate gradient algorithm for obtaining the mean, which can significantly reduce the complexity and increase stability by relying on the Jacobi preconditioner that proves to fit the EP characteristics very well. For the variance, we use a simple approximation based on linear regression of the Gram channel matrix. Numerical studies on the Rayleigh-fading channel and on a realistic 3GPP channel model reveal the efficiency of the proposed scheme, which offers an attractive performance-complexity tradeoff and even outperforms the original EP detector in high multi-user inference cases where the matrix inversion becomes numerically unstable.

Blind Channel Estimation and Joint Symbol Detection with Data-Driven Factor Graphs

We investigate the application of the factor graph framework for blind joint channel estimation and symbol detection on time-variant linear inter-symbol interference channels. In particular, we consider the expectation maximization (EM) algorithm for maximum likelihood estimation, which typically suffers from high complexity as it requires the computation of the symbol-wise posterior distributions in every iteration. We address this issue by efficiently approximating the posteriors using the belief propagation (BP) algorithm on a suitable factor graph. By interweaving the iterations of BP and EM, the detection complexity can be further reduced to a single BP iteration per EM step. In addition, we propose a data-driven version of our algorithm that introduces momentum in the BP updates and learns a suitable EM parameter update schedule, thereby significantly improving the performance-complexity tradeoff with a few offline training samples. Our numerical experiments demonstrate the excellent performance of the proposed blind detector and show that it even outperforms coherent BP detection in high signal-to-noise scenarios.

Approximate Maximum a Posteriori Carrier Phase Estimator for Wiener Phase Noise Channels using Belief Propagation

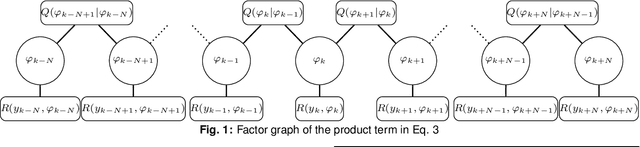
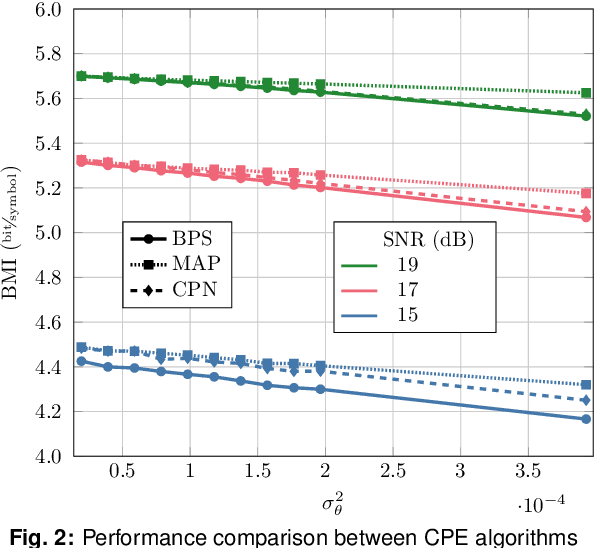
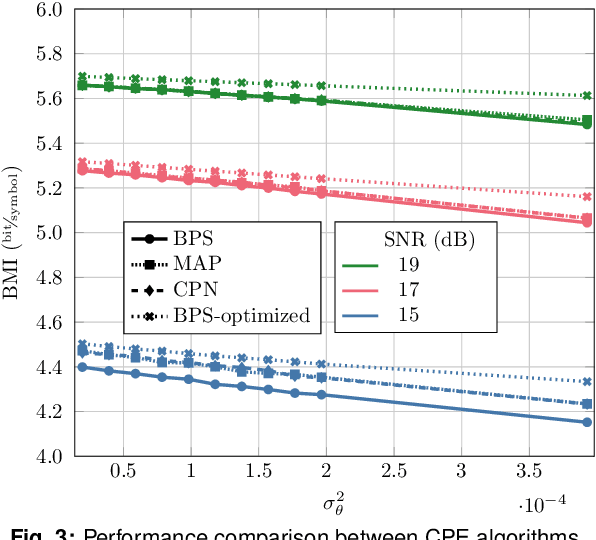
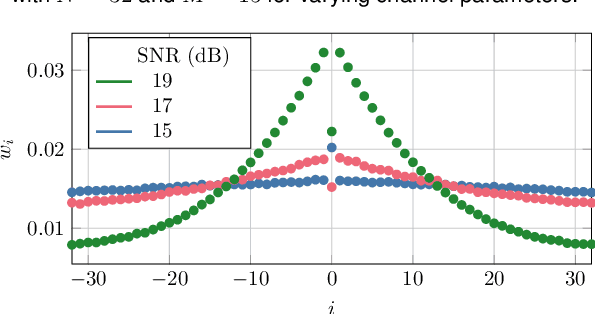
The blind phase search (BPS) algorithm for carrier phase estimation is known to have sub-optimal performance for probabilistically shaped constellations. We present a belief propagation based approximate maximum a posteriori carrier phase estimator and compare its performance with the standard and an improved BPS algorithm.

Local Message Passing on Frustrated Systems

Message passing on factor graphs is a powerful framework for probabilistic inference, which finds important applications in various scientific domains. The most wide-spread message passing scheme is the sum-product algorithm (SPA) which gives exact results on trees but often fails on graphs with many small cycles. We search for an alternative message passing algorithm that works particularly well on such cyclic graphs. Therefore, we challenge the extrinsic principle of the SPA, which loses its objective on graphs with cycles. We further replace the local SPA message update rule at the factor nodes of the underlying graph with a generic mapping, which is optimized in a data-driven fashion. These modifications lead to a considerable improvement in performance while preserving the simplicity of the SPA. We evaluate our method for two classes of cyclic graphs: the 2x2 fully connected Ising grid and factor graphs for symbol detection on linear communication channels with inter-symbol interference. To enable the method for large graphs as they occur in practical applications, we develop a novel loss function that is inspired by the Bethe approximation from statistical physics and allows for training in an unsupervised fashion.

Structural Optimization of Factor Graphs for Symbol Detection via Continuous Clustering and Machine Learning

We propose a novel method to optimize the structure of factor graphs for graph-based inference. As an example inference task, we consider symbol detection on linear inter-symbol interference channels. The factor graph framework has the potential to yield low-complexity symbol detectors. However, the sum-product algorithm on cyclic factor graphs is suboptimal and its performance is highly sensitive to the underlying graph. Therefore, we optimize the structure of the underlying factor graphs in an end-to-end manner using machine learning. For that purpose, we transform the structural optimization into a clustering problem of low-degree factor nodes that incorporates the known channel model into the optimization. Furthermore, we study the combination of this approach with neural belief propagation, yielding near-maximum a posteriori symbol detection performance for specific channels.

Low-complexity Near-optimum Symbol Detection Based on Neural Enhancement of Factor Graphs

We consider the application of the factor graph framework for symbol detection on linear inter-symbol interference channels. Based on the Ungerboeck observation model, a detection algorithm with appealing complexity properties can be derived. However, since the underlying factor graph contains cycles, the sum-product algorithm (SPA) yields a suboptimal algorithm. In this paper, we develop and evaluate efficient strategies to improve the performance of the factor graph-based symbol detection by means of neural enhancement. In particular, we consider neural belief propagation as an effective way to mitigate the effect of cycles within the factor graph. We also investigate the application of factor node generalizations and pruning techniques. By applying a generic preprocessor to the channel output, we propose a simple technique to vary the underlying factor graph in every SPA iteration. Using this dynamic factor graph transition, we intend to preserve the extrinsic nature of the SPA messages which is otherwise impaired due to cycles. Simulation results show that the proposed methods can massively improve the detection performance, even approaching the maximum a posteriori performance for various transmission scenarios, while preserving a complexity which is linear in both the block length and the channel memory.

Neural Enhancement of Factor Graph-based Symbol Detection

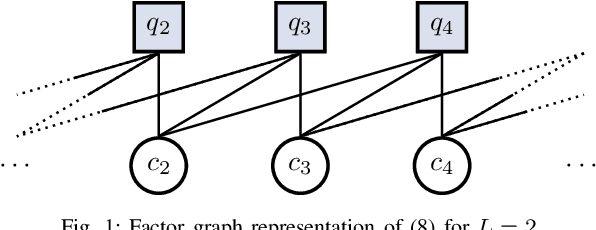
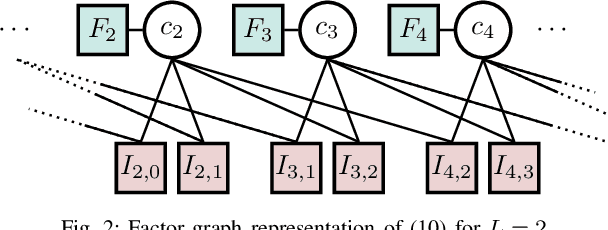
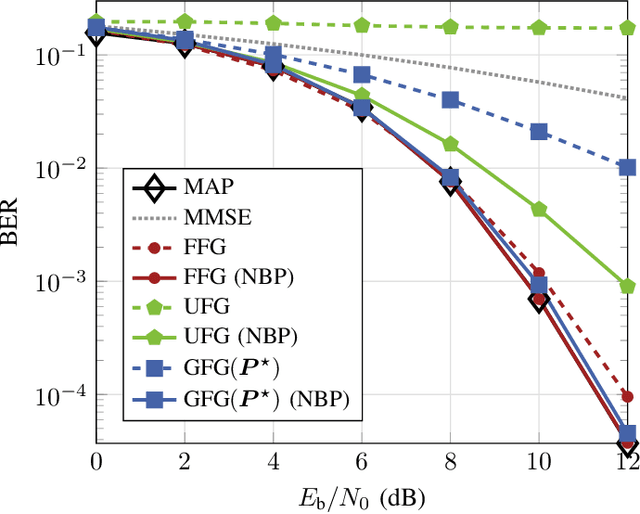
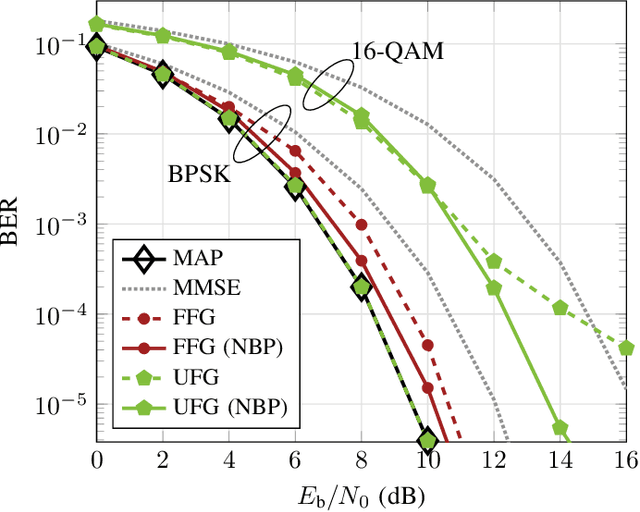
We study the application of the factor graph framework for symbol detection on linear inter-symbol interference channels. Cyclic factor graphs have the potential to yield low-complexity symbol detectors, but are suboptimal if the ubiquitous sum-product algorithm is applied. In this paper, we present and evaluate strategies to improve the performance of cyclic factor graph-based symbol detection algorithms by means of neural enhancement. In particular, we apply neural belief propagation as an effective way to counteract the effect of cycles within the factor graph. We further propose the application and optimization of a linear preprocessor of the channel output. By modifying the observation model, the preprocessing can effectively change the underlying factor graph, thereby significantly improving the detection performance as well as reducing the complexity.