Weighted Leave-One-Out Cross Validation

We present a weighted version of Leave-One-Out (LOO) cross-validation for estimating the Integrated Squared Error (ISE) when approximating an unknown function by a predictor that depends linearly on evaluations of the function over a finite collection of sites. The method relies on the construction of the best linear estimator of the squared prediction error at an arbitrary unsampled site based on squared LOO residuals, assuming that the function is a realization of a Gaussian Process (GP). A theoretical analysis of performance of the ISE estimator is presented, and robustness with respect to the choice of the GP kernel is investigated first analytically, then through numerical examples. Overall, the estimation of ISE is significantly more precise than with classical, unweighted, LOO cross validation. Application to model selection is briefly considered through examples.

Fast Screening Rules for Optimal Design via Quadratic Lasso Reformulation

The problems of Lasso regression and optimal design of experiments share a critical property: their optimal solutions are typically \emph{sparse}, i.e., only a small fraction of the optimal variables are non-zero. Therefore, the identification of the support of an optimal solution reduces the dimensionality of the problem and can yield a substantial simplification of the calculations. It has recently been shown that linear regression with a \emph{squared} $\ell_1$-norm sparsity-inducing penalty is equivalent to an optimal experimental design problem. In this work, we use this equivalence to derive safe screening rules that can be used to discard inessential samples. Compared to previously existing rules, the new tests are much faster to compute, especially for problems involving a parameter space of high dimension, and can be used dynamically within any iterative solver, with negligible computational overhead. Moreover, we show how an existing homotopy algorithm to compute the regularization path of the lasso method can be reparametrized with respect to the squared $\ell_1$-penalty. This allows the computation of a Bayes $c$-optimal design in a finite number of steps and can be several orders of magnitude faster than standard first-order algorithms. The efficiency of the new screening rules and of the homotopy algorithm are demonstrated on different examples based on real data.

Active Discrimination Learning for Gaussian Process Models

The paper covers the design and analysis of experiments to discriminate between two Gaussian process models, such as those widely used in computer experiments, kriging, sensor location and machine learning. Two frameworks are considered. First, we study sequential constructions, where successive design (observation) points are selected, either as additional points to an existing design or from the beginning of observation. The selection relies on the maximisation of the difference between the symmetric Kullback Leibler divergences for the two models, which depends on the observations, or on the mean squared error of both models, which does not. Then, we consider static criteria, such as the familiar log-likelihood ratios and the Fr\'echet distance between the covariance functions of the two models. Other distance-based criteria, simpler to compute than previous ones, are also introduced, for which, considering the framework of approximate design, a necessary condition for the optimality of a design measure is provided. The paper includes a study of the mathematical links between different criteria and numerical illustrations are provided.

Quasi-uniform designs with optimal and near-optimal uniformity constant

A design is a collection of distinct points in a given set $X$, which is assumed to be a compact subset of $R^d$, and the mesh-ratio of a design is the ratio of its fill distance to its separation radius. The uniformity constant of a sequence of nested designs is the smallest upper bound for the mesh-ratios of the designs. We derive a lower bound on this uniformity constant and show that a simple greedy construction achieves this lower bound. We then extend this scheme to allow more flexibility in the design construction.

Performance analysis of greedy algorithms for minimising a Maximum Mean Discrepancy

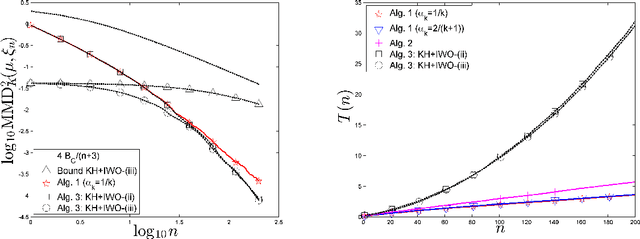
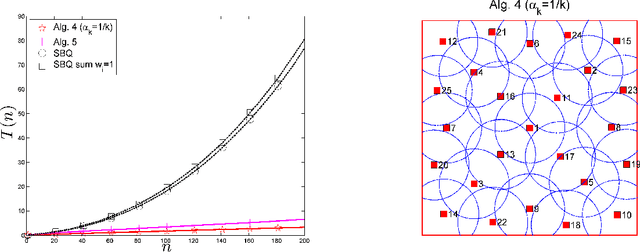
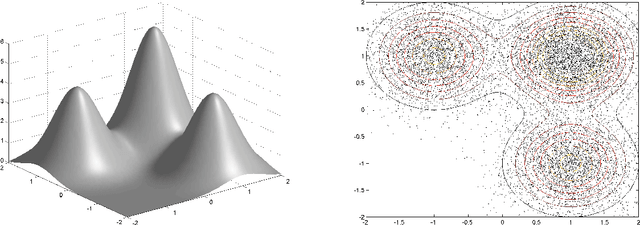
We analyse the performance of several iterative algorithms for the quantisation of a probability measure $\mu$, based on the minimisation of a Maximum Mean Discrepancy (MMD). Our analysis includes kernel herding, greedy MMD minimisation and Sequential Bayesian Quadrature (SBQ). We show that the finite-sample-size approximation error, measured by the MMD, decreases as $1/n$ for SBQ and also for kernel herding and greedy MMD minimisation when using a suitable step-size sequence. The upper bound on the approximation error is slightly better for SBQ, but the other methods are significantly faster, with a computational cost that increases only linearly with the number of points selected. This is illustrated by two numerical examples, with the target measure $\mu$ being uniform (a space-filling design application) and with $\mu$ a Gaussian mixture.