Solving optimal stopping problems with Deep Q-Learning

We propose a reinforcement learning (RL) approach to model optimal exercise strategies for option-type products. We pursue the RL avenue in order to learn the optimal action-value function of the underlying stopping problem. In addition to retrieving the optimal Q-function at any time step, one can also price the contract at inception. We first discuss the standard setting with one exercise right, and later extend this framework to the case of multiple stopping opportunities in the presence of constraints. We propose to approximate the Q-function with a deep neural network, which does not require the specification of basis functions as in the least-squares Monte Carlo framework and is scalable to higher dimensions. We derive a lower bound on the option price obtained from the trained neural network and an upper bound from the dual formulation of the stopping problem, which can also be expressed in terms of the Q-function. Our methodology is illustrated with examples covering the pricing of swing options.

Distributional Random Forests: Heterogeneity Adjustment and Multivariate Distributional Regression

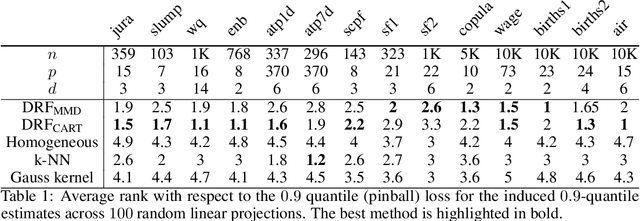
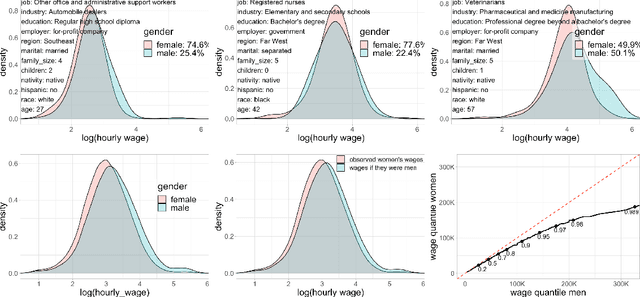
We propose an adaptation of the Random Forest algorithm to estimate the conditional distribution of a possibly multivariate response. We suggest a new splitting criterion based on the MMD two-sample test, which is suitable for detecting heterogeneity in multivariate distributions. The weights provided by the forest can be conveniently used as an input to other methods in order to locally solve various learning problems. The code is available as \texttt{R}-package \texttt{drf}.