Noise2Self: Blind Denoising by Self-Supervision

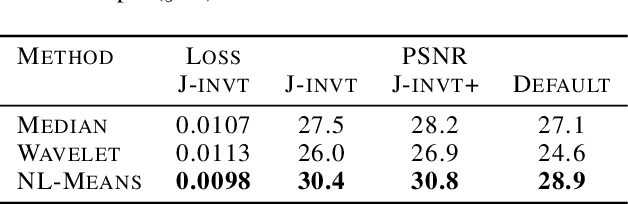
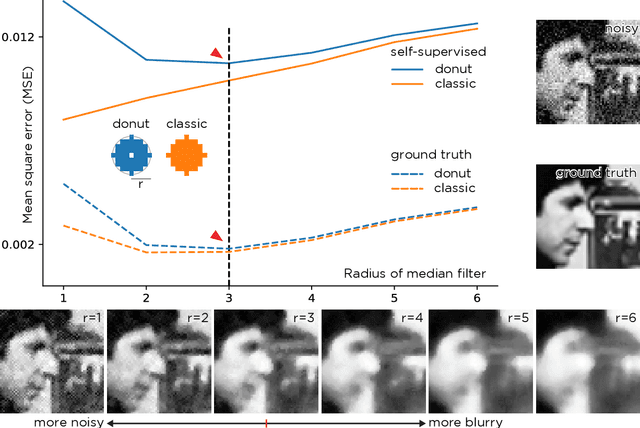
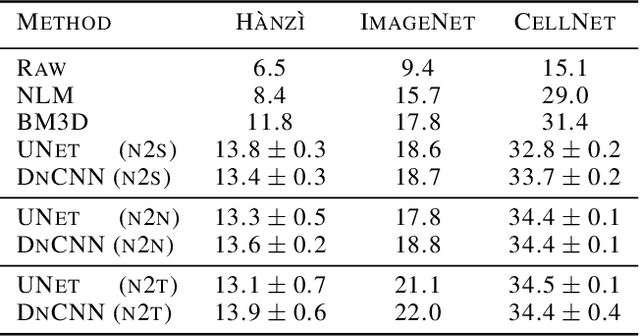
We propose a general framework for denoising high-dimensional measurements which requires no prior on the signal, no estimate of the noise, and no clean training data. The only assumption is that the noise exhibits statistical independence across different dimensions of the measurement. Moreover, our framework is not restricted to a particular denoising model. We show how it can be used to calibrate any parameterised denoising algorithm, from the single hyperparameter of a median filter to the millions of weights of a deep neural network. We demonstrate this on natural image and microscopy data, where we exploit noise independence between pixels, and on single-cell gene expression data, where we exploit independence between detections of individual molecules. Finally, we prove a theoretical lower bound on the performance of an optimal denoiser. This framework generalizes recent work on training neural nets from noisy images and on cross-validation for matrix factorization.

Isotropic reconstruction of 3D fluorescence microscopy images using convolutional neural networks

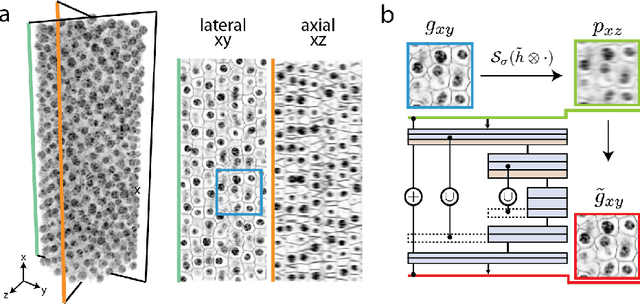
Fluorescence microscopy images usually show severe anisotropy in axial versus lateral resolution. This hampers downstream processing, i.e. the automatic extraction of quantitative biological data. While deconvolution methods and other techniques to address this problem exist, they are either time consuming to apply or limited in their ability to remove anisotropy. We propose a method to recover isotropic resolution from readily acquired anisotropic data. We achieve this using a convolutional neural network that is trained end-to-end from the same anisotropic body of data we later apply the network to. The network effectively learns to restore the full isotropic resolution by restoring the image under a trained, sample specific image prior. We apply our method to $3$ synthetic and $3$ real datasets and show that our results improve on results from deconvolution and state-of-the-art super-resolution techniques. Finally, we demonstrate that a standard 3D segmentation pipeline performs on the output of our network with comparable accuracy as on the full isotropic data.