Liyun Zeng
Sparse Learning and Class Probability Estimation with Weighted Support Vector Machines
Dec 17, 2023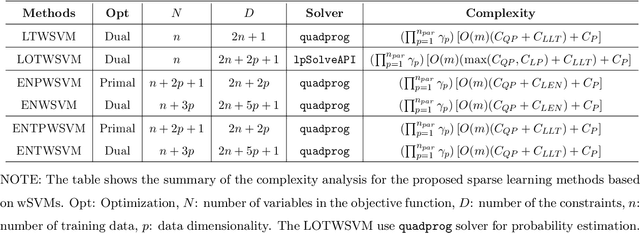
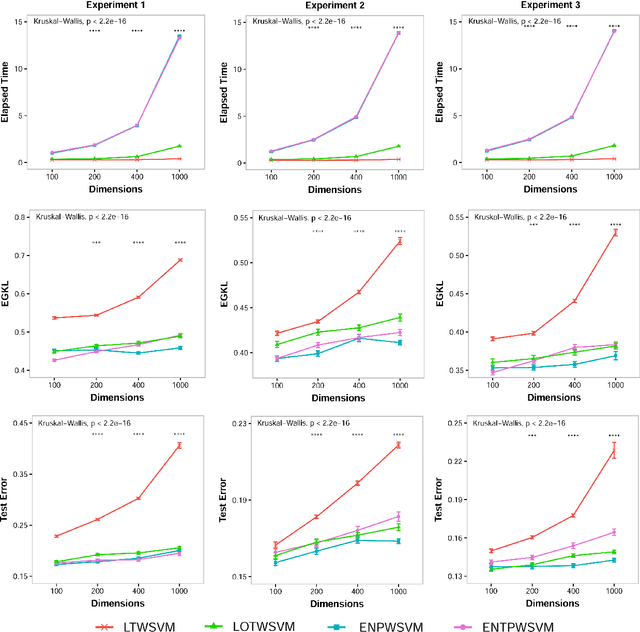
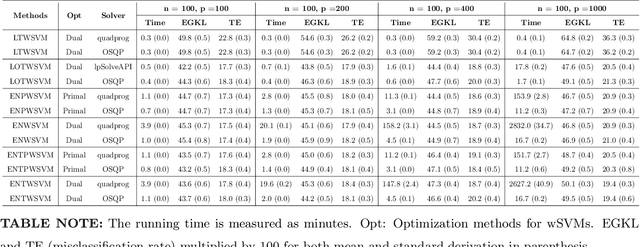
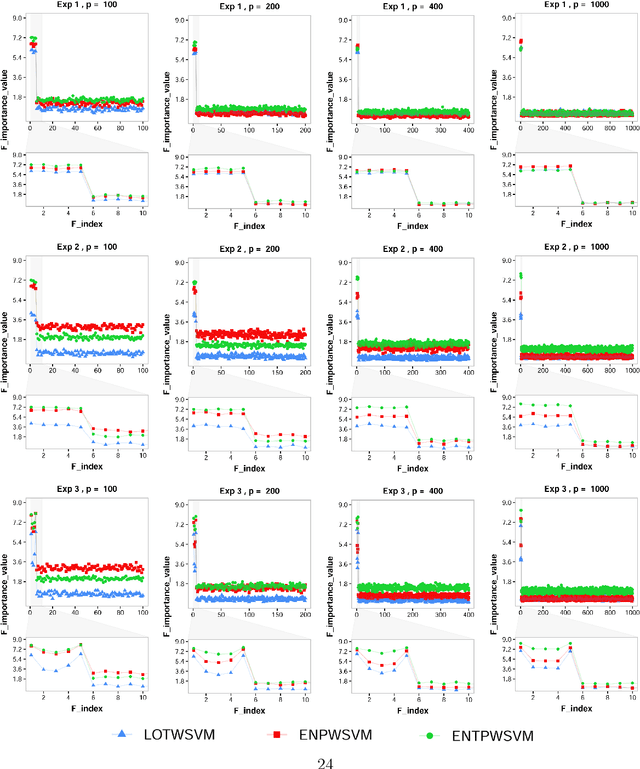
Abstract:Classification and probability estimation have broad applications in modern machine learning and data science applications, including biology, medicine, engineering, and computer science. The recent development of a class of weighted Support Vector Machines (wSVMs) has shown great values in robustly predicting the class probability and classification for various problems with high accuracy. The current framework is based on the $\ell^2$-norm regularized binary wSVMs optimization problem, which only works with dense features and has poor performance at sparse features with redundant noise in most real applications. The sparse learning process requires a prescreen of the important variables for each binary wSVMs for accurately estimating pairwise conditional probability. In this paper, we proposed novel wSVMs frameworks that incorporate automatic variable selection with accurate probability estimation for sparse learning problems. We developed efficient algorithms for effective variable selection for solving either the $\ell^1$-norm or elastic net regularized binary wSVMs optimization problems. The binary class probability is then estimated either by the $\ell^2$-norm regularized wSVMs framework with selected variables or by elastic net regularized wSVMs directly. The two-step approach of $\ell^1$-norm followed by $\ell^2$-norm wSVMs show a great advantage in both automatic variable selection and reliable probability estimators with the most efficient time. The elastic net regularized wSVMs offer the best performance in terms of variable selection and probability estimation with the additional advantage of variable grouping in the compensation of more computation time for high dimensional problems. The proposed wSVMs-based sparse learning methods have wide applications and can be further extended to $K$-class problems through ensemble learning.
Robust Brain MRI Image Classification with SIBOW-SVM
Nov 15, 2023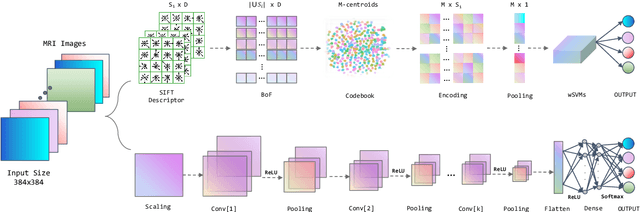
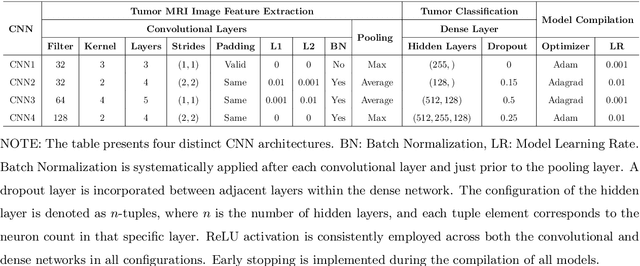
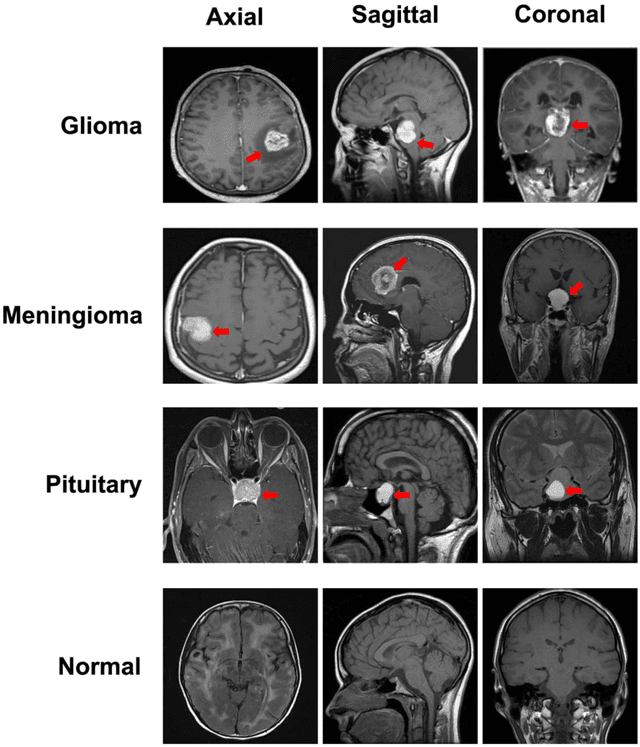
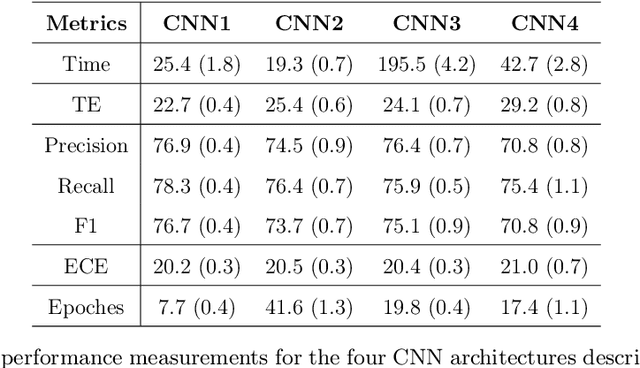
Abstract:The majority of primary Central Nervous System (CNS) tumors in the brain are among the most aggressive diseases affecting humans. Early detection of brain tumor types, whether benign or malignant, glial or non-glial, is critical for cancer prevention and treatment, ultimately improving human life expectancy. Magnetic Resonance Imaging (MRI) stands as the most effective technique to detect brain tumors by generating comprehensive brain images through scans. However, human examination can be error-prone and inefficient due to the complexity, size, and location variability of brain tumors. Recently, automated classification techniques using machine learning (ML) methods, such as Convolutional Neural Network (CNN), have demonstrated significantly higher accuracy than manual screening, while maintaining low computational costs. Nonetheless, deep learning-based image classification methods, including CNN, face challenges in estimating class probabilities without proper model calibration. In this paper, we propose a novel brain tumor image classification method, called SIBOW-SVM, which integrates the Bag-of-Features (BoF) model with SIFT feature extraction and weighted Support Vector Machines (wSVMs). This new approach effectively captures hidden image features, enabling the differentiation of various tumor types and accurate label predictions. Additionally, the SIBOW-SVM is able to estimate the probabilities of images belonging to each class, thereby providing high-confidence classification decisions. We have also developed scalable and parallelable algorithms to facilitate the practical implementation of SIBOW-SVM for massive images. As a benchmark, we apply the SIBOW-SVM to a public data set of brain tumor MRI images containing four classes: glioma, meningioma, pituitary, and normal. Our results show that the new method outperforms state-of-the-art methods, including CNN.
Linear Algorithms for Nonparametric Multiclass Probability Estimation
Jun 03, 2022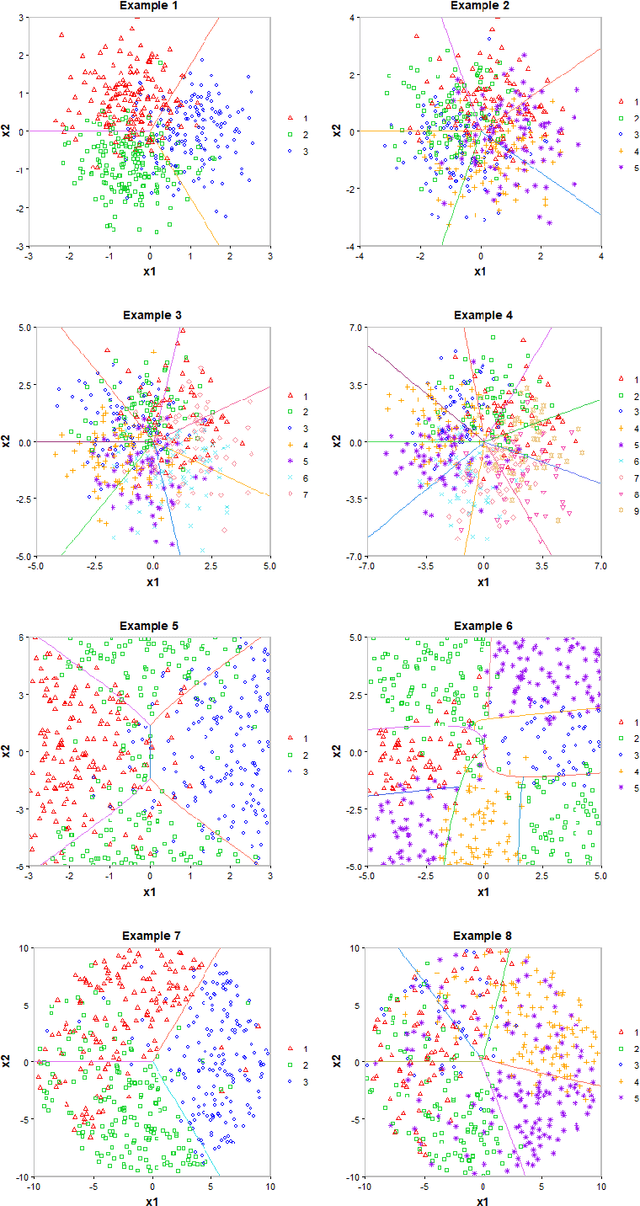

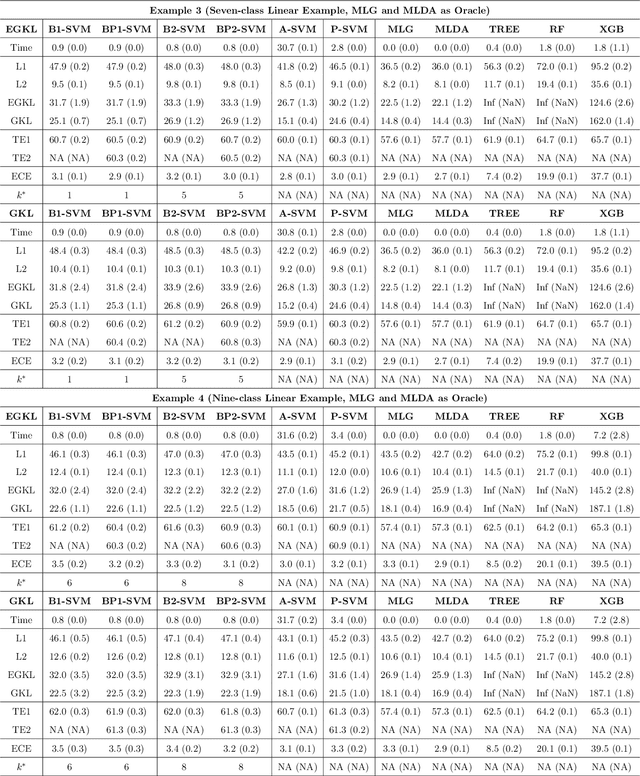
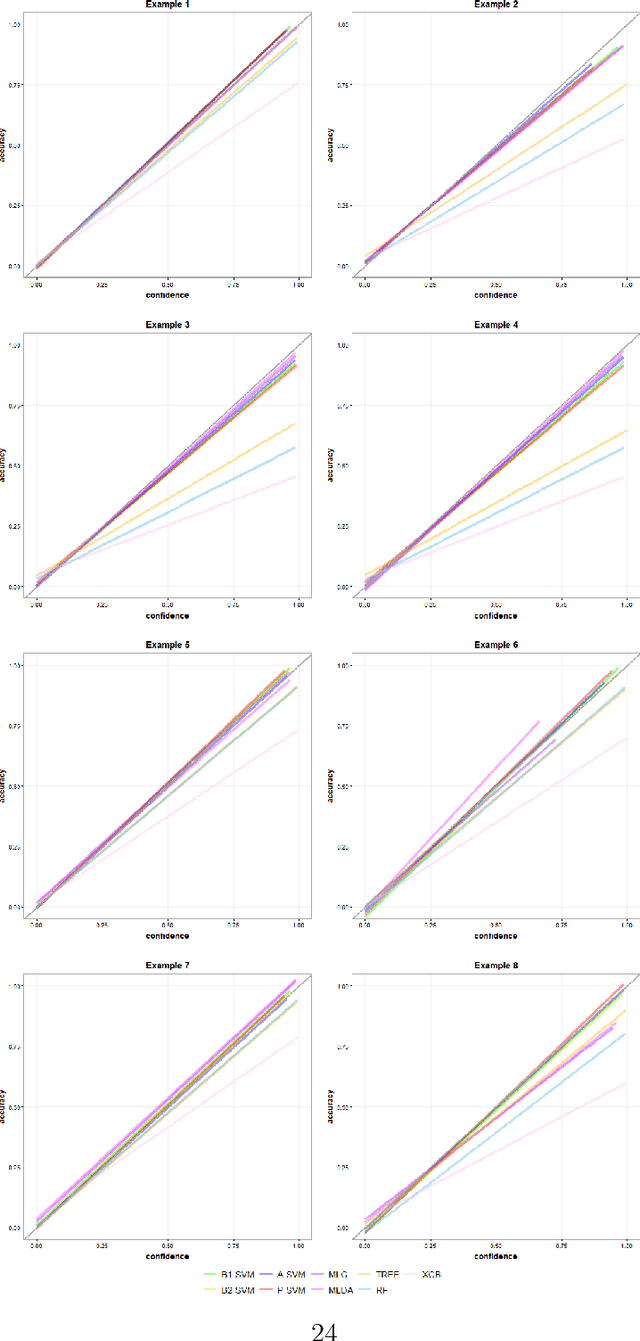
Abstract:Multiclass probability estimation is the problem of estimating conditional probabilities of a data point belonging to a class given its covariate information. It has broad applications in statistical analysis and data science. Recently a class of weighted Support Vector Machines (wSVMs) has been developed to estimate class probabilities through ensemble learning for $K$-class problems (Wu, Zhang and Liu, 2010; Wang, Zhang and Wu, 2019), where $K$ is the number of classes. The estimators are robust and achieve high accuracy for probability estimation, but their learning is implemented through pairwise coupling, which demands polynomial time in $K$. In this paper, we propose two new learning schemes, the baseline learning and the One-vs-All (OVA) learning, to further improve wSVMs in terms of computational efficiency and estimation accuracy. In particular, the baseline learning has optimal computational complexity in the sense that it is linear in $K$. Though not being most efficient in computation, the OVA offers the best estimation accuracy among all the procedures under comparison. The resulting estimators are distribution-free and shown to be consistent. We further conduct extensive numerical experiments to demonstrate finite sample performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge