Sparse Learning and Class Probability Estimation with Weighted Support Vector Machines
Paper and Code
Dec 17, 2023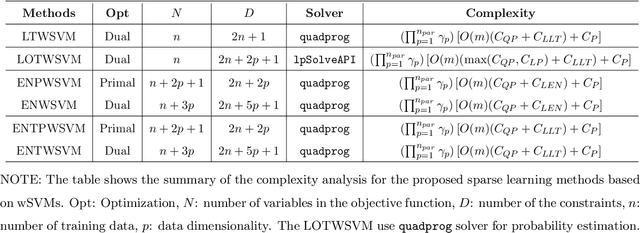
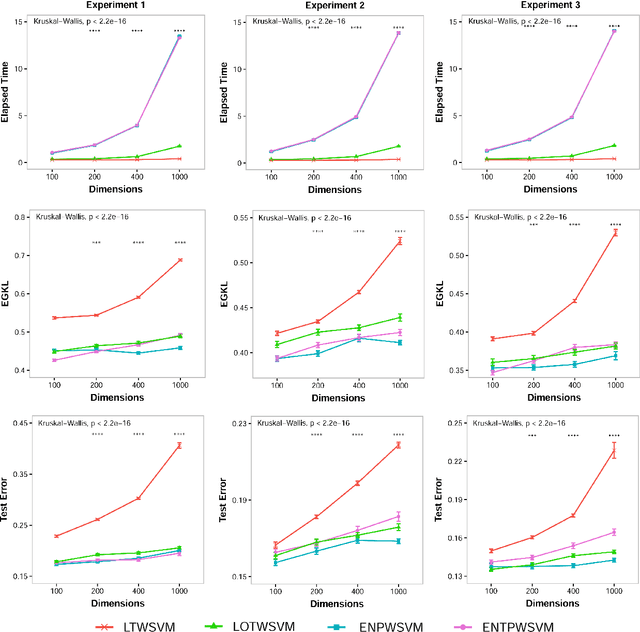
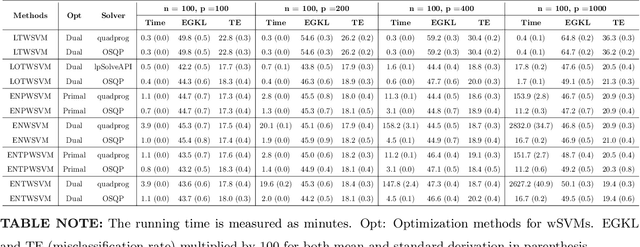
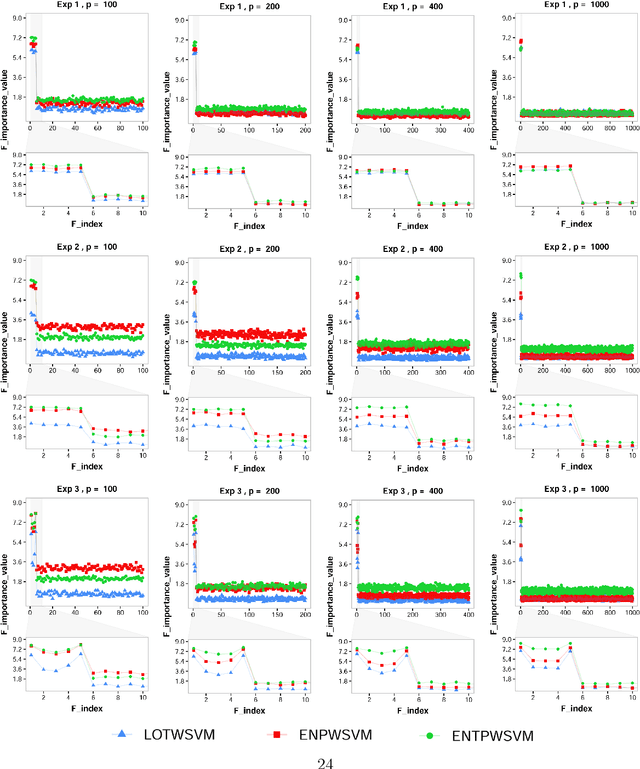
Classification and probability estimation have broad applications in modern machine learning and data science applications, including biology, medicine, engineering, and computer science. The recent development of a class of weighted Support Vector Machines (wSVMs) has shown great values in robustly predicting the class probability and classification for various problems with high accuracy. The current framework is based on the $\ell^2$-norm regularized binary wSVMs optimization problem, which only works with dense features and has poor performance at sparse features with redundant noise in most real applications. The sparse learning process requires a prescreen of the important variables for each binary wSVMs for accurately estimating pairwise conditional probability. In this paper, we proposed novel wSVMs frameworks that incorporate automatic variable selection with accurate probability estimation for sparse learning problems. We developed efficient algorithms for effective variable selection for solving either the $\ell^1$-norm or elastic net regularized binary wSVMs optimization problems. The binary class probability is then estimated either by the $\ell^2$-norm regularized wSVMs framework with selected variables or by elastic net regularized wSVMs directly. The two-step approach of $\ell^1$-norm followed by $\ell^2$-norm wSVMs show a great advantage in both automatic variable selection and reliable probability estimators with the most efficient time. The elastic net regularized wSVMs offer the best performance in terms of variable selection and probability estimation with the additional advantage of variable grouping in the compensation of more computation time for high dimensional problems. The proposed wSVMs-based sparse learning methods have wide applications and can be further extended to $K$-class problems through ensemble learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge