Ling Xiang
Boolean Product Graph Neural Networks
Sep 21, 2024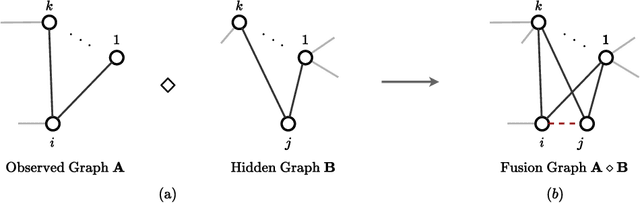
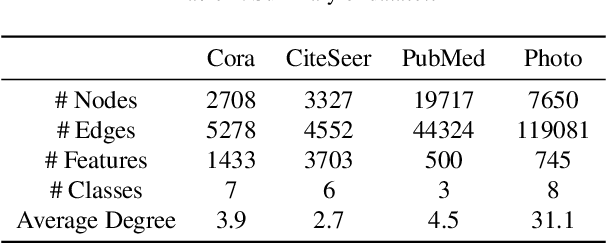
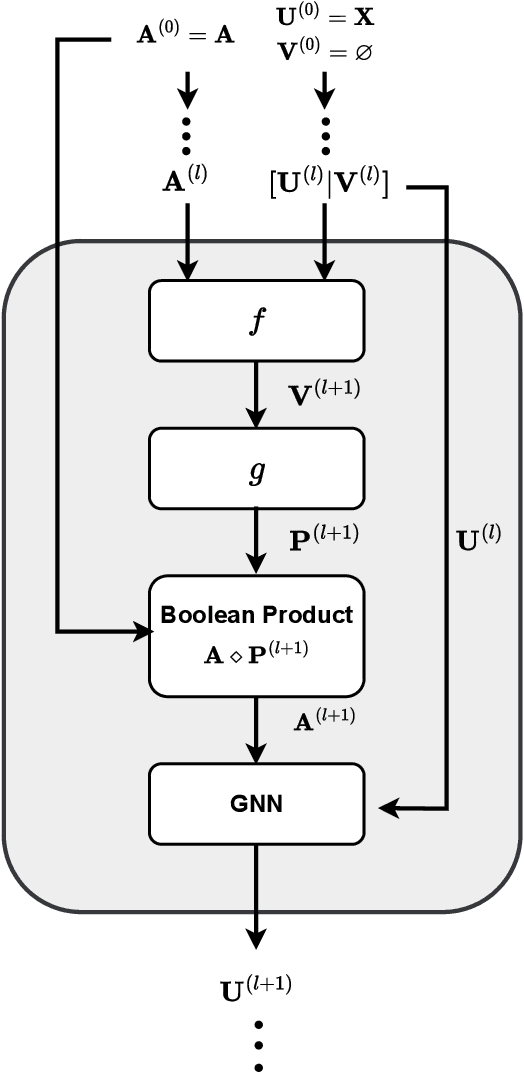
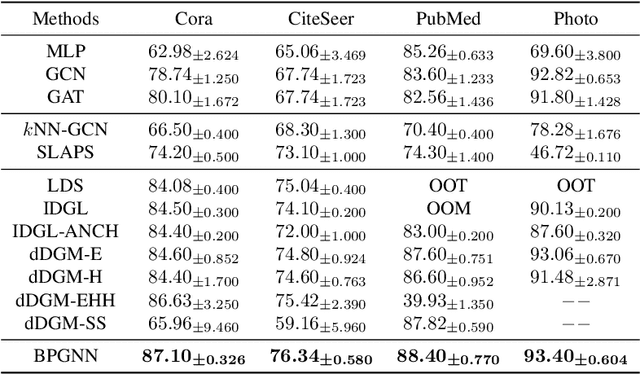
Abstract:Graph Neural Networks (GNNs) have recently achieved significant success, with a key operation involving the aggregation of information from neighboring nodes. Substantial researchers have focused on defining neighbors for aggregation, predominantly based on observed adjacency matrices. However, in many scenarios, the explicitly given graphs contain noise, which can be amplified during the messages-passing process. Therefore, many researchers have turned their attention to latent graph inference, specifically learning a parametric graph. To mitigate fluctuations in latent graph structure learning, this paper proposes a novel Boolean product-based graph residual connection in GNNs to link the latent graph and the original graph. It computes the Boolean product between the latent graph and the original graph at each layer to correct the learning process. The Boolean product between two adjacency matrices is equivalent to triangle detection. Accordingly, the proposed Boolean product graph neural networks can be interpreted as discovering triangular cliques from the original and the latent graph. We validate the proposed method in benchmark datasets and demonstrate its ability to enhance the performance and robustness of GNNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge