Ensemble Transport Filter via Optimized Maximum Mean Discrepancy

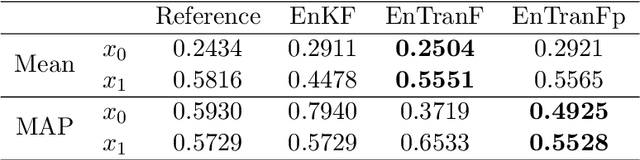
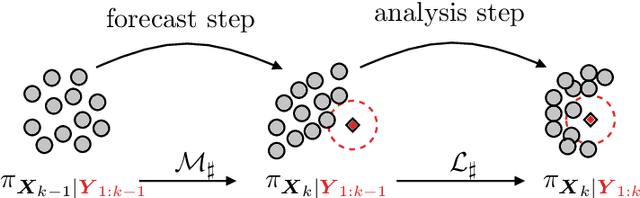
In this paper, we present a new ensemble-based filter method by reconstructing the analysis step of the particle filter through a transport map, which directly transports prior particles to posterior particles. The transport map is constructed through an optimization problem described by the Maximum Mean Discrepancy loss function, which matches the expectation information of the approximated posterior and reference posterior. The proposed method inherits the accurate estimation of the posterior distribution from particle filtering. To improve the robustness of Maximum Mean Discrepancy, a variance penalty term is used to guide the optimization. It prioritizes minimizing the discrepancy between the expectations of highly informative statistics for the approximated and reference posteriors. The penalty term significantly enhances the robustness of the proposed method and leads to a better approximation of the posterior. A few numerical examples are presented to illustrate the advantage of the proposed method over the ensemble Kalman filter.

Conditional variational autoencoder with Gaussian process regression recognition for parametric models

In this article, we present a data-driven method for parametric models with noisy observation data. Gaussian process regression based reduced order modeling (GPR-based ROM) can realize fast online predictions without using equations in the offline stage. However, GPR-based ROM does not perform well for complex systems since POD projection are naturally linear. Conditional variational autoencoder (CVAE) can address this issue via nonlinear neural networks but it has more model complexity, which poses challenges for training and tuning hyperparameters. To this end, we propose a framework of CVAE with Gaussian process regression recognition (CVAE-GPRR). The proposed method consists of a recognition model and a likelihood model. In the recognition model, we first extract low-dimensional features from data by POD to filter the redundant information with high frequency. And then a non-parametric model GPR is used to learn the map from parameters to POD latent variables, which can also alleviate the impact of noise. CVAE-GPRR can achieve the similar accuracy to CVAE but with fewer parameters. In the likelihood model, neural networks are used to reconstruct data. Besides the samples of POD latent variables and input parameters, physical variables are also added as the inputs to make predictions in the whole physical space. This can not be achieved by either GPR-based ROM or CVAE. Moreover, the numerical results show that CVAE-GPRR may alleviate the overfitting issue in CVAE.