Ensemble Transport Filter via Optimized Maximum Mean Discrepancy
Paper and Code
Jul 16, 2024
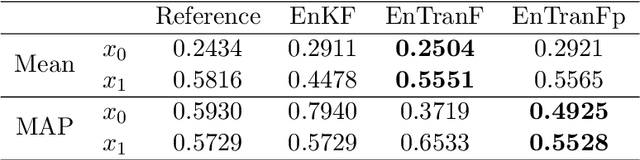
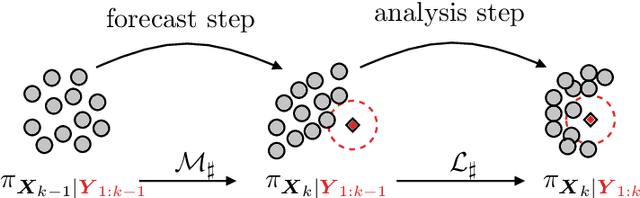

In this paper, we present a new ensemble-based filter method by reconstructing the analysis step of the particle filter through a transport map, which directly transports prior particles to posterior particles. The transport map is constructed through an optimization problem described by the Maximum Mean Discrepancy loss function, which matches the expectation information of the approximated posterior and reference posterior. The proposed method inherits the accurate estimation of the posterior distribution from particle filtering. To improve the robustness of Maximum Mean Discrepancy, a variance penalty term is used to guide the optimization. It prioritizes minimizing the discrepancy between the expectations of highly informative statistics for the approximated and reference posteriors. The penalty term significantly enhances the robustness of the proposed method and leads to a better approximation of the posterior. A few numerical examples are presented to illustrate the advantage of the proposed method over the ensemble Kalman filter.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge