Lihong Feng
Subspace-Distance-Enabled Active Learning for Efficient Data-Driven Model Reduction of Parametric Dynamical Systems
May 01, 2025Abstract:In situations where the solution of a high-fidelity dynamical system needs to be evaluated repeatedly, over a vast pool of parametric configurations and in absence of access to the underlying governing equations, data-driven model reduction techniques are preferable. We propose a novel active learning approach to build a parametric data-driven reduced-order model (ROM) by greedily picking the most important parameter samples from the parameter domain. As a result, during the ROM construction phase, the number of high-fidelity solutions dynamically grow in a principled fashion. The high-fidelity solution snapshots are expressed in several parameter-specific linear subspaces, with the help of proper orthogonal decomposition (POD), and the relative distance between these subspaces is used as a guiding mechanism to perform active learning. For successfully achieving this, we provide a distance measure to evaluate the similarity between pairs of linear subspaces with different dimensions, and also show that this distance measure is a metric. The usability of the proposed subspace-distance-enabled active learning (SDE-AL) framework is demonstrated by augmenting two existing non-intrusive reduced-order modeling approaches, and providing their active-learning-driven (ActLearn) extensions, namely, SDE-ActLearn-POD-KSNN, and SDE-ActLearn-POD-NN. Furthermore, we report positive results for two parametric physical models, highlighting the efficiency of the proposed SDE-AL approach.
Interpretable Spatial-Temporal Fusion Transformers: Multi-Output Prediction for Parametric Dynamical Systems with Time-Varying Inputs
May 01, 2025


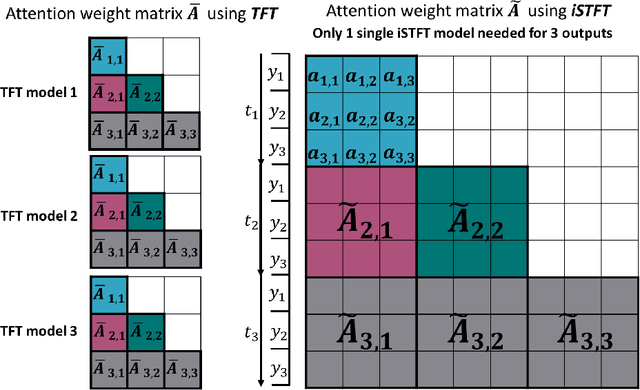
Abstract:We explore the promising performance of a transformer model in predicting outputs of parametric dynamical systems with external time-varying input signals. The outputs of such systems vary not only with physical parameters but also with external time-varying input signals. Accurately catching the dynamics of such systems is challenging. We have adapted and extended an existing transformer model for single output prediction to a multiple-output transformer that is able to predict multiple output responses of these systems. The multiple-output transformer generalizes the interpretability of the original transformer. The generalized interpretable attention weight matrix explores not only the temporal correlations in the sequence, but also the interactions between the multiple outputs, providing explanation for the spatial correlation in the output domain. This multiple-output transformer accurately predicts the sequence of multiple outputs, regardless of the nonlinearity of the system and the dimensionality of the parameter space.
Data-Augmented Predictive Deep Neural Network: Enhancing the extrapolation capabilities of non-intrusive surrogate models
Oct 17, 2024



Abstract:Numerically solving a large parametric nonlinear dynamical system is challenging due to its high complexity and the high computational costs. In recent years, machine-learning-aided surrogates are being actively researched. However, many methods fail in accurately generalizing in the entire time interval $[0, T]$, when the training data is available only in a training time interval $[0, T_0]$, with $T_0<T$. To improve the extrapolation capabilities of the surrogate models in the entire time domain, we propose a new deep learning framework, where kernel dynamic mode decomposition (KDMD) is employed to evolve the dynamics of the latent space generated by the encoder part of a convolutional autoencoder (CAE). After adding the KDMD-decoder-extrapolated data into the original data set, we train the CAE along with a feed-forward deep neural network using the augmented data. The trained network can predict future states outside the training time interval at any out-of-training parameter samples. The proposed method is tested on two numerical examples: a FitzHugh-Nagumo model and a model of incompressible flow past a cylinder. Numerical results show accurate and fast prediction performance in both the time and the parameter domain.
Active-Learning-Driven Surrogate Modeling for Efficient Simulation of Parametric Nonlinear Systems
Jun 09, 2023



Abstract:When repeated evaluations for varying parameter configurations of a high-fidelity physical model are required, surrogate modeling techniques based on model order reduction are desired. In absence of the governing equations describing the dynamics, we need to construct the parametric reduced-order surrogate model in a non-intrusive fashion. In this setting, the usual residual-based error estimate for optimal parameter sampling associated with the reduced basis method is not directly available. Our work provides a non-intrusive optimality criterion to efficiently populate the parameter snapshots, thereby, enabling us to effectively construct a parametric surrogate model. We consider separate parameter-specific proper orthogonal decomposition (POD) subspaces and propose an active-learning-driven surrogate model using kernel-based shallow neural networks, abbreviated as ActLearn-POD-KSNN surrogate model. To demonstrate the validity of our proposed ideas, we present numerical experiments using two physical models, namely Burgers' equation and shallow water equations. Both the models have mixed -- convective and diffusive -- effects within their respective parameter domains, with each of them dominating in certain regions. The proposed ActLearn-POD-KSNN surrogate model efficiently predicts the solution at new parameter locations, even for a setting with multiple interacting shock profiles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge