Leonardo Alexandre
Integrating Statistical Significance and Discriminative Power in Pattern Discovery
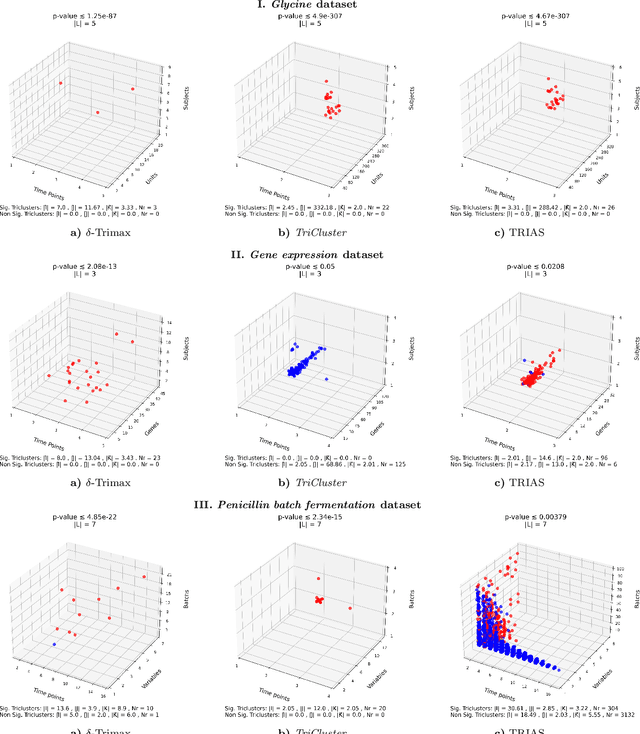
Jan 22, 2024Abstract:Pattern discovery plays a central role in both descriptive and predictive tasks across multiple domains. Actionable patterns must meet rigorous statistical significance criteria and, in the presence of target variables, further uphold discriminative power. Our work addresses the underexplored area of guiding pattern discovery by integrating statistical significance and discriminative power criteria into state-of-the-art algorithms while preserving pattern quality. We also address how pattern quality thresholds, imposed by some algorithms, can be rectified to accommodate these additional criteria. To test the proposed methodology, we select the triclustering task as the guiding pattern discovery case and extend well-known greedy and multi-objective optimization triclustering algorithms, $\delta$-Trimax and TriGen, that use various pattern quality criteria, such as Mean Squared Residual (MSR), Least Squared Lines (LSL), and Multi Slope Measure (MSL). Results from three case studies show the role of the proposed methodology in discovering patterns with pronounced improvements of discriminative power and statistical significance without quality deterioration, highlighting its importance in supervisedly guiding the search. Although the proposed methodology is motivated over multivariate time series data, it can be straightforwardly extended to pattern discovery tasks involving multivariate, N-way (N>3), transactional, and sequential data structures. Availability: The code is freely available at https://github.com/JupitersMight/MOF_Triclustering under the MIT license.
TriSig: Assessing the statistical significance of triclusters
Jun 12, 2023
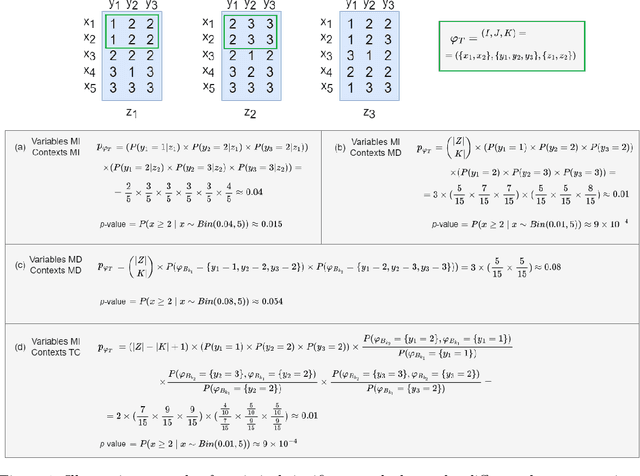

Abstract:Tensor data analysis allows researchers to uncover novel patterns and relationships that cannot be obtained from matrix data alone. The information inferred from the patterns provides valuable insights into disease progression, bioproduction processes, weather fluctuations, and group dynamics. However, spurious and redundant patterns hamper this process. This work aims at proposing a statistical frame to assess the probability of patterns in tensor data to deviate from null expectations, extending well-established principles for assessing the statistical significance of patterns in matrix data. A comprehensive discussion on binomial testing for false positive discoveries is entailed at the light of: variable dependencies, temporal dependencies and misalignments, and \textit{p}-value corrections under the Benjamini-Hochberg procedure. Results gathered from the application of state-of-the-art triclustering algorithms over distinct real-world case studies in biochemical and biotechnological domains confer validity to the proposed statistical frame while revealing vulnerabilities of some triclustering searches. The proposed assessment can be incorporated into existing triclustering algorithms to mitigate false positive/spurious discoveries and further prune the search space, reducing their computational complexity. Availability: The code is freely available at https://github.com/JupitersMight/TriSig under the MIT license.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge