TriSig: Assessing the statistical significance of triclusters
Paper and Code
Jun 12, 2023
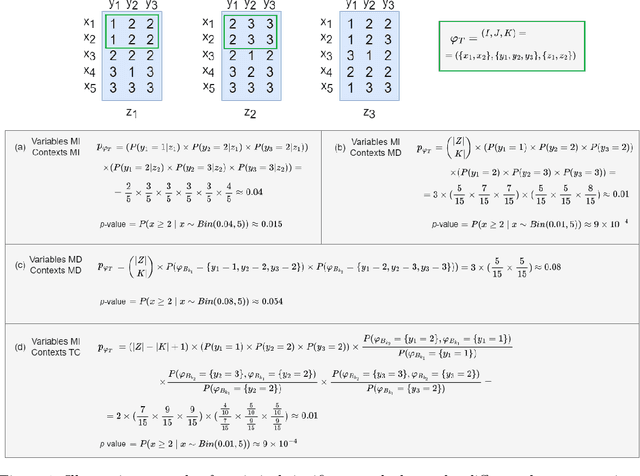

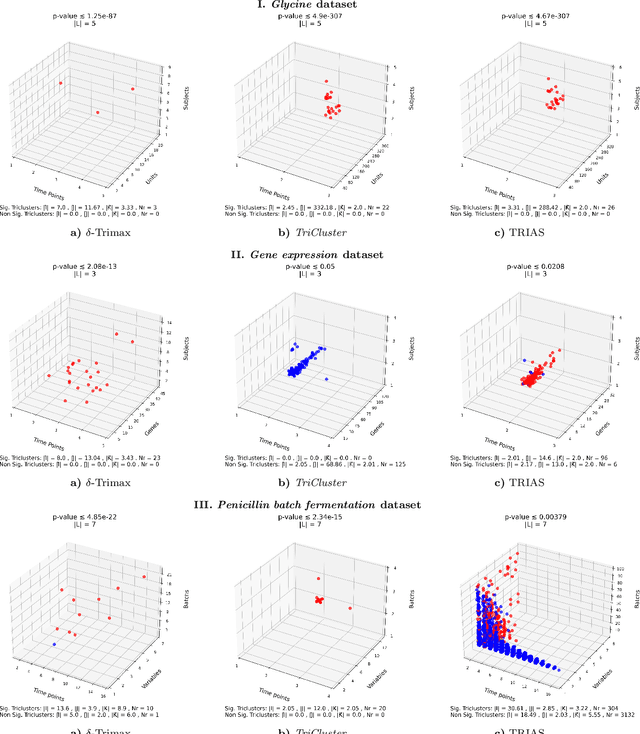
Tensor data analysis allows researchers to uncover novel patterns and relationships that cannot be obtained from matrix data alone. The information inferred from the patterns provides valuable insights into disease progression, bioproduction processes, weather fluctuations, and group dynamics. However, spurious and redundant patterns hamper this process. This work aims at proposing a statistical frame to assess the probability of patterns in tensor data to deviate from null expectations, extending well-established principles for assessing the statistical significance of patterns in matrix data. A comprehensive discussion on binomial testing for false positive discoveries is entailed at the light of: variable dependencies, temporal dependencies and misalignments, and \textit{p}-value corrections under the Benjamini-Hochberg procedure. Results gathered from the application of state-of-the-art triclustering algorithms over distinct real-world case studies in biochemical and biotechnological domains confer validity to the proposed statistical frame while revealing vulnerabilities of some triclustering searches. The proposed assessment can be incorporated into existing triclustering algorithms to mitigate false positive/spurious discoveries and further prune the search space, reducing their computational complexity. Availability: The code is freely available at https://github.com/JupitersMight/TriSig under the MIT license.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge