Parallel Transport Unfolding: A Connection-based Manifold Learning Approach

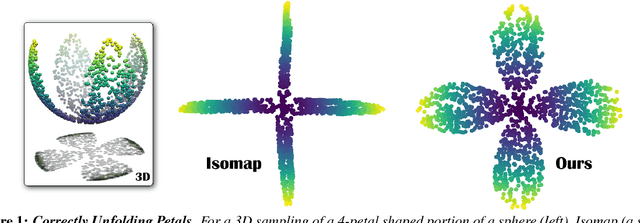
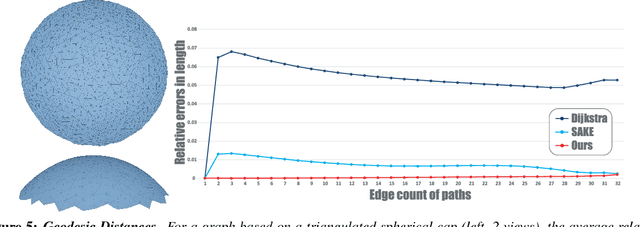
Manifold learning offers nonlinear dimensionality reduction of high-dimensional datasets. In this paper, we bring geometry processing to bear on manifold learning by introducing a new approach based on metric connection for generating a quasi-isometric, low-dimensional mapping from a sparse and irregular sampling of an arbitrary manifold embedded in a high-dimensional space. Geodesic distances of discrete paths over the input pointset are evaluated through "parallel transport unfolding" (PTU) to offer robustness to poor sampling and arbitrary topology. Our new geometric procedure exhibits the same strong resilience to noise as one of the staples of manifold learning, the Isomap algorithm, as it also exploits all pairwise geodesic distances to compute a low-dimensional embedding. While Isomap is limited to geodesically-convex sampled domains, parallel transport unfolding does not suffer from this crippling limitation, resulting in an improved robustness to irregularity and voids in the sampling. Moreover, it involves only simple linear algebra, significantly improves the accuracy of all pairwise geodesic distance approximations, and has the same computational complexity as Isomap. Finally, we show that our connection-based distance estimation can be used for faster variants of Isomap such as L-Isomap.