A Physics-Informed Machine Learning for Electricity Markets: A NYISO Case Study

This paper addresses the challenge of efficiently solving the optimal power flow problem in real-time electricity markets. The proposed solution, named Physics-Informed Market-Aware Active Set learning OPF (PIMA-AS-OPF), leverages physical constraints and market properties to ensure physical and economic feasibility of market-clearing outcomes. Specifically, PIMA-AS-OPF employs the active set learning technique and expands its capabilities to account for curtailment in load or renewable power generation, which is a common challenge in real-world power systems. The core of PIMA-AS-OPF is a fully-connected neural network that takes the net load and the system topology as input. The outputs of this neural network include active constraints such as saturated generators and transmission lines, as well as non-zero load shedding and wind curtailments. These outputs allow for reducing the original market-clearing optimization to a system of linear equations, which can be solved efficiently and yield both the dispatch decisions and the locational marginal prices (LMPs). The dispatch decisions and LMPs are then tested for their feasibility with respect to the requirements for efficient market-clearing results. The accuracy and scalability of the proposed method is tested on a realistic 1814-bus NYISO system with current and future renewable energy penetration levels.

Machine Learning for Electricity Market Clearing

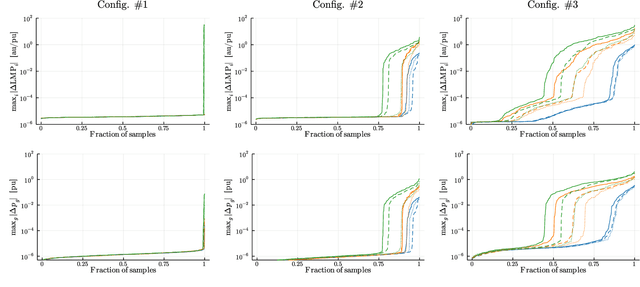
This paper seeks to design a machine learning twin of the optimal power flow (OPF) optimization, which is used in market-clearing procedures by wholesale electricity markets. The motivation for the proposed approach stems from the need to obtain the digital twin, which is much faster than the original, while also being sufficiently accurate and producing consistent generation dispatches and locational marginal prices (LMPs), which are primal and dual solutions of the OPF optimization, respectively. Availability of market-clearing tools based on this approach will enable computationally tractable evaluation of multiple dispatch scenarios under a given unit commitment. Rather than direct solution of OPF, the Karush-Kuhn-Tucker (KKT) conditions for the OPF problem in question may be written, and in parallel the LMPs of generators and loads may be expressed in terms of the OPF Lagrangian multipliers. Also, taking advantage of the practical fact that many of the Lagrangian multipliers associated with lines will be zero (thermal limits are not binding), we build and train an ML scheme which maps flexible resources (loads and renewables) to the binding lines, and supplement it with an efficient power-grid aware linear map to optimal dispatch and LMPs. The scheme is validated and illustrated on IEEE models. We also report a trade of analysis between quality of the reconstruction and number of samples needed to train the model.

Model Reduction of Swing Equations with Physics Informed PDE

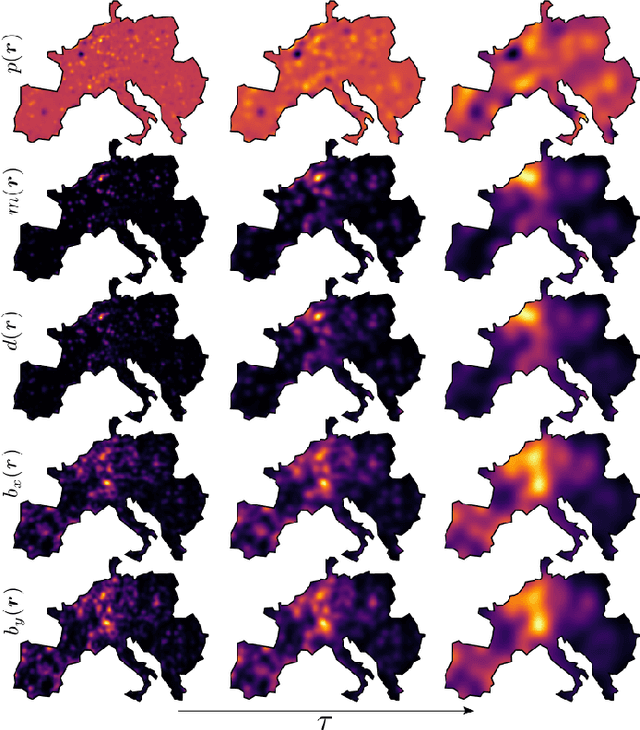
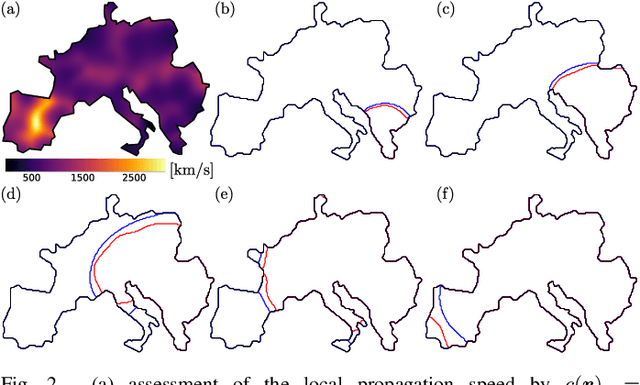
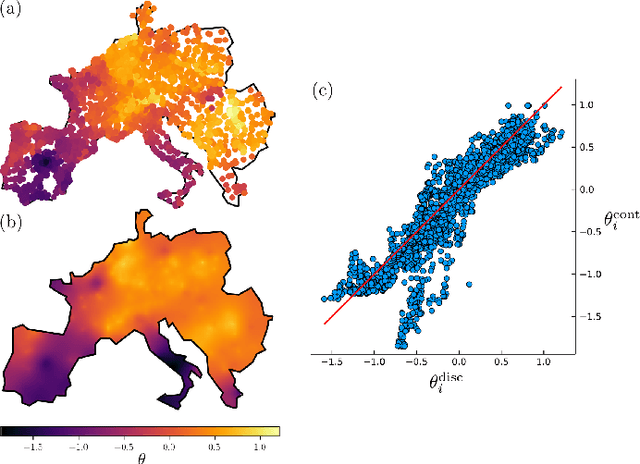
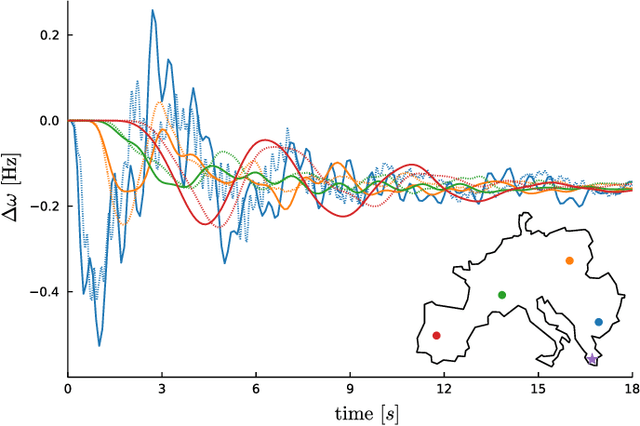
This manuscript is the first step towards building a robust and efficient model reduction methodology to capture transient dynamics in a transmission level electric power system. Such dynamics is normally modeled on seconds-to-tens-of-seconds time scales by the so-called swing equations, which are ordinary differential equations defined on a spatially discrete model of the power grid. We suggest, following Seymlyen (1974) and Thorpe, Seyler and Phadke (1999), to map the swing equations onto a linear, inhomogeneous Partial Differential Equation (PDE) of parabolic type in two space and one time dimensions with time-independent coefficients and properly defined boundary conditions. The continuous two-dimensional spatial domain is defined by a geographical map of the area served by the power grid, and associated with the PDE coefficients derived from smoothed graph-Laplacian of susceptances, machine inertia and damping. Inhomogeneous source terms represent spatially distributed injection/consumption of power. We illustrate our method on PanTaGruEl (Pan-European Transmission Grid and ELectricity generation model). We show that, when properly coarse-grained, i.e. with the PDE coefficients and source terms extracted from a spatial convolution procedure of the respective discrete coefficients in the swing equations, the resulting PDE reproduces faithfully and efficiently the original swing dynamics. We finally discuss future extensions of this work, where the presented PDE-based reduced modeling will initialize a physics-informed machine learning approach for real-time modeling, $n-1$ feasibility assessment and transient stability analysis of power systems.

Embedding Power Flow into Machine Learning for Parameter and State Estimation

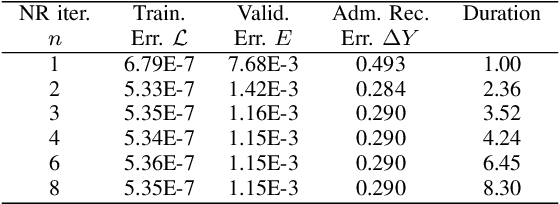
Modern state and parameter estimations in power systems consist of two stages: the outer problem of minimizing the mismatch between network observation and prediction over the network parameters, and the inner problem of predicting the system state for given values of the parameters. The standard solution of the combined problem is iterative: (a) set the parameters, e.g. to priors on the power line characteristics, (b) map input observation to prediction of the output, (c) compute the mismatch between predicted and observed output, (d) make a gradient descent step in the space of parameters to minimize the mismatch, and loop back to (a). We show how modern Machine Learning (ML), and specifically training guided by automatic differentiation, allows to resolve the iterative loop more efficiently. Moreover, we extend the scheme to the case of incomplete observations, where Phasor Measurement Units (reporting real and reactive powers, voltage and phase) are available only at the generators (PV buses), while loads (PQ buses) report (via SCADA controls) only active and reactive powers. Considering it from the implementation perspective, our methodology of resolving the parameter and state estimation problem can be viewed as embedding of the Power Flow (PF) solver into the training loop of the Machine Learning framework (PyTorch, in this study). We argue that this embedding can help to resolve high-level optimization problems in power system operations and planning.

Physics-Informed Graphical Neural Network for Parameter & State Estimations in Power Systems

Parameter Estimation (PE) and State Estimation (SE) are the most wide-spread tasks in the system engineering. They need to be done automatically, fast and frequently, as measurements arrive. Deep Learning (DL) holds the promise of tackling the challenge, however in so far, as PE and SE in power systems is concerned, (a) DL did not win trust of the system operators because of the lack of the physics of electricity based, interpretations and (b) DL remained illusive in the operational regimes were data is scarce. To address this, we present a hybrid scheme which embeds physics modeling of power systems into Graphical Neural Networks (GNN), therefore empowering system operators with a reliable and explainable real-time predictions which can then be used to control the critical infrastructure. To enable progress towards trustworthy DL for PE and SE, we build a physics-informed method, named Power-GNN, which reconstructs physical, thus interpretable, parameters within Effective Power Flow (EPF) models, such as admittances of effective power lines, and NN parameters, representing implicitly unobserved elements of the system. In our experiments, we test the Power-GNN on different realistic power networks, including these with thousands of loads and hundreds of generators. We show that the Power-GNN outperforms vanilla NN scheme unaware of the EPF physics.