A Physics-Informed Machine Learning for Electricity Markets: A NYISO Case Study

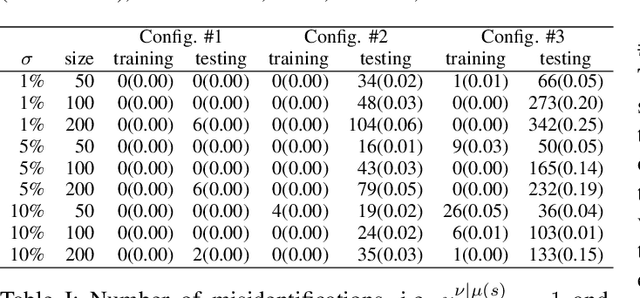
This paper addresses the challenge of efficiently solving the optimal power flow problem in real-time electricity markets. The proposed solution, named Physics-Informed Market-Aware Active Set learning OPF (PIMA-AS-OPF), leverages physical constraints and market properties to ensure physical and economic feasibility of market-clearing outcomes. Specifically, PIMA-AS-OPF employs the active set learning technique and expands its capabilities to account for curtailment in load or renewable power generation, which is a common challenge in real-world power systems. The core of PIMA-AS-OPF is a fully-connected neural network that takes the net load and the system topology as input. The outputs of this neural network include active constraints such as saturated generators and transmission lines, as well as non-zero load shedding and wind curtailments. These outputs allow for reducing the original market-clearing optimization to a system of linear equations, which can be solved efficiently and yield both the dispatch decisions and the locational marginal prices (LMPs). The dispatch decisions and LMPs are then tested for their feasibility with respect to the requirements for efficient market-clearing results. The accuracy and scalability of the proposed method is tested on a realistic 1814-bus NYISO system with current and future renewable energy penetration levels.

Machine Learning for Electricity Market Clearing

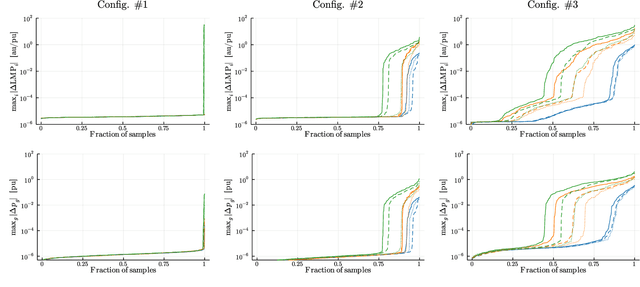
This paper seeks to design a machine learning twin of the optimal power flow (OPF) optimization, which is used in market-clearing procedures by wholesale electricity markets. The motivation for the proposed approach stems from the need to obtain the digital twin, which is much faster than the original, while also being sufficiently accurate and producing consistent generation dispatches and locational marginal prices (LMPs), which are primal and dual solutions of the OPF optimization, respectively. Availability of market-clearing tools based on this approach will enable computationally tractable evaluation of multiple dispatch scenarios under a given unit commitment. Rather than direct solution of OPF, the Karush-Kuhn-Tucker (KKT) conditions for the OPF problem in question may be written, and in parallel the LMPs of generators and loads may be expressed in terms of the OPF Lagrangian multipliers. Also, taking advantage of the practical fact that many of the Lagrangian multipliers associated with lines will be zero (thermal limits are not binding), we build and train an ML scheme which maps flexible resources (loads and renewables) to the binding lines, and supplement it with an efficient power-grid aware linear map to optimal dispatch and LMPs. The scheme is validated and illustrated on IEEE models. We also report a trade of analysis between quality of the reconstruction and number of samples needed to train the model.