Profiling checkpointing schedules in adjoint ST-AD

Checkpointing is a cornerstone of data-flow reversal in adjoint algorithmic differentiation. Checkpointing is a storage/recomputation trade-off that can be applied at different levels, one of which being the call tree. We are looking for good placements of checkpoints onto the call tree of a given application, to reduce run time and memory footprint of its adjoint. There is no known optimal solution to this problem other than a combinatorial search on all placements. We propose a heuristics based on run-time profiling of the adjoint code. We describe implementation of this profiling tool in an existing source-transformation AD tool. We demonstrate the interest of this approach on test cases taken from the MITgcm ocean and atmospheric global circulation model. We discuss the limitations of our approach and propose directions to lift them.

Understanding Automatic Differentiation Pitfalls

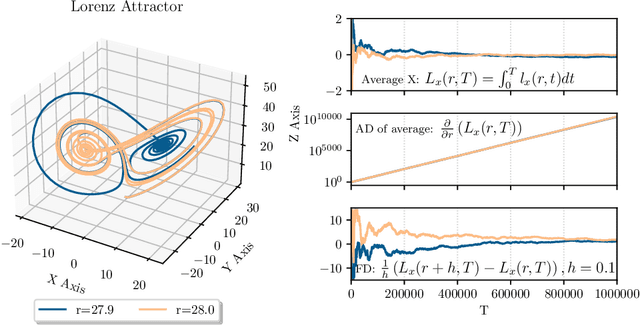
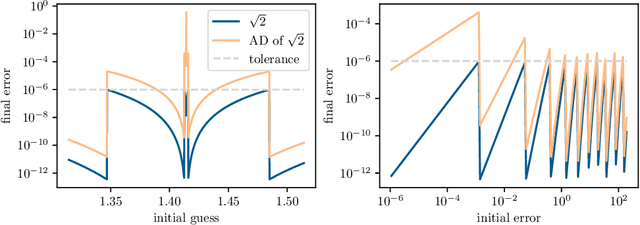
Automatic differentiation, also known as backpropagation, AD, autodiff, or algorithmic differentiation, is a popular technique for computing derivatives of computer programs accurately and efficiently. Sometimes, however, the derivatives computed by AD could be interpreted as incorrect. These pitfalls occur systematically across tools and approaches. In this paper we broadly categorize problematic usages of AD and illustrate each category with examples such as chaos, time-averaged oscillations, discretizations, fixed-point loops, lookup tables, and linear solvers. We also review debugging techniques and their effectiveness in these situations. With this article we hope to help readers avoid unexpected behavior, detect problems more easily when they occur, and have more realistic expectations from AD tools.

Source-to-Source Automatic Differentiation of OpenMP Parallel Loops

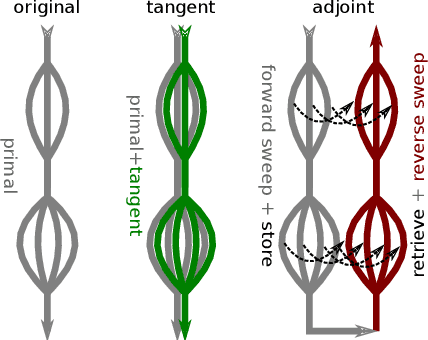
This paper presents our work toward correct and efficient automatic differentiation of OpenMP parallel worksharing loops in forward and reverse mode. Automatic differentiation is a method to obtain gradients of numerical programs, which are crucial in optimization, uncertainty quantification, and machine learning. The computational cost to compute gradients is a common bottleneck in practice. For applications that are parallelized for multicore CPUs or GPUs using OpenMP, one also wishes to compute the gradients in parallel. We propose a framework to reason about the correctness of the generated derivative code, from which we justify our OpenMP extension to the differentiation model. We implement this model in the automatic differentiation tool Tapenade and present test cases that are differentiated following our extended differentiation procedure. Performance of the generated derivative programs in forward and reverse mode is better than sequential, although our reverse mode often scales worse than the input programs.