Estimating the age-conditioned average treatment effects curves: An application for assessing load-management strategies in the NBA

In the realm of competitive sports, understanding the performance dynamics of athletes, represented by the age curve (showing progression, peak, and decline), is vital. Our research introduces a novel framework for quantifying age-specific treatment effects, enhancing the granularity of performance trajectory analysis. Firstly, we propose a methodology for estimating the age curve using game-level data, diverging from traditional season-level data approaches, and tackling its inherent complexities with a meta-learner framework that leverages advanced machine learning models. This approach uncovers intricate non-linear patterns missed by existing methods. Secondly, our framework enables the identification of causal effects, allowing for a detailed examination of age curves under various conditions. By defining the Age-Conditioned Treatment Effect (ACTE), we facilitate the exploration of causal relationships regarding treatment impacts at specific ages. Finally, applying this methodology to study the effects of rest days on performance metrics, particularly across different ages, offers valuable insights into load management strategies' effectiveness. Our findings underscore the importance of tailored rest periods, highlighting their positive impact on athlete performance and suggesting a reevaluation of current management practices for optimizing athlete performance.

Doubly Robust Estimator for Off-Policy Evaluation with Large Action Spaces

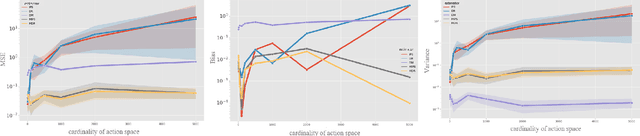
We study Off-Policy Evaluation (OPE) in contextual bandit settings with large action spaces. The benchmark estimators suffer from severe bias and variance tradeoffs. Parametric approaches suffer from bias due to difficulty specifying the correct model, whereas ones with importance weight suffer from variance. To overcome these limitations, Marginalized Inverse Propensity Scoring (MIPS) was proposed to mitigate the estimator's variance via embeddings of an action. To make the estimator more accurate, we propose the doubly robust estimator of MIPS called the Marginalized Doubly Robust (MDR) estimator. Theoretical analysis shows that the proposed estimator is unbiased under weaker assumptions than MIPS while maintaining variance reduction against IPS, which was the main advantage of MIPS. The empirical experiment verifies the supremacy of MDR against existing estimators.