Improving the Sampling Strategy in KernelSHAP

Shapley values are a popular model-agnostic explanation framework for explaining predictions made by complex machine learning models. The framework provides feature contribution scores that sum to the predicted response and represent each feature's importance. The computation of exact Shapley values is computationally expensive due to estimating an exponential amount of non-trivial conditional expectations. The KernelSHAP framework enables us to approximate the Shapley values using a sampled subset of weighted conditional expectations. We propose three main novel contributions: a stabilizing technique to reduce the variance of the weights in the current state-of-the-art strategy, a novel weighing scheme that corrects the Shapley kernel weights based on sampled subsets, and a straightforward strategy that includes the important subsets and integrates them with the corrected Shapley kernel weights. We compare these new approximation strategies against existing ones by evaluating their Shapley value accuracy as a function of the number of subsets. The results demonstrate that our sampling strategies significantly enhance the accuracy of the approximated Shapley value explanations, making them more reliable in practical applications. This work provides valuable insights and practical recommendations for researchers and practitioners seeking to implement Shapley value-based explainability of their models.

Precision of Individual Shapley Value Explanations

Shapley values are extensively used in explainable artificial intelligence (XAI) as a framework to explain predictions made by complex machine learning (ML) models. In this work, we focus on conditional Shapley values for predictive models fitted to tabular data and explain the prediction $f(\boldsymbol{x}^{*})$ for a single observation $\boldsymbol{x}^{*}$ at the time. Numerous Shapley value estimation methods have been proposed and empirically compared on an average basis in the XAI literature. However, less focus has been devoted to analyzing the precision of the Shapley value explanations on an individual basis. We extend our work in Olsen et al. (2023) by demonstrating and discussing that the explanations are systematically less precise for observations on the outer region of the training data distribution for all used estimation methods. This is expected from a statistical point of view, but to the best of our knowledge, it has not been systematically addressed in the Shapley value literature. This is crucial knowledge for Shapley values practitioners, who should be more careful in applying these observations' corresponding Shapley value explanations.

A Comparative Study of Methods for Estimating Conditional Shapley Values and When to Use Them

Shapley values originated in cooperative game theory but are extensively used today as a model-agnostic explanation framework to explain predictions made by complex machine learning models in the industry and academia. There are several algorithmic approaches for computing different versions of Shapley value explanations. Here, we focus on conditional Shapley values for predictive models fitted to tabular data. Estimating precise conditional Shapley values is difficult as they require the estimation of non-trivial conditional expectations. In this article, we develop new methods, extend earlier proposed approaches, and systematize the new refined and existing methods into different method classes for comparison and evaluation. The method classes use either Monte Carlo integration or regression to model the conditional expectations. We conduct extensive simulation studies to evaluate how precisely the different method classes estimate the conditional expectations, and thereby the conditional Shapley values, for different setups. We also apply the methods to several real-world data experiments and provide recommendations for when to use the different method classes and approaches. Roughly speaking, we recommend using parametric methods when we can specify the data distribution almost correctly, as they generally produce the most accurate Shapley value explanations. When the distribution is unknown, both generative methods and regression models with a similar form as the underlying predictive model are good and stable options. Regression-based methods are often slow to train but produce the Shapley value explanations quickly once trained. The vice versa is true for Monte Carlo-based methods, making the different methods appropriate in different practical situations.

Using Shapley Values and Variational Autoencoders to Explain Predictive Models with Dependent Mixed Features

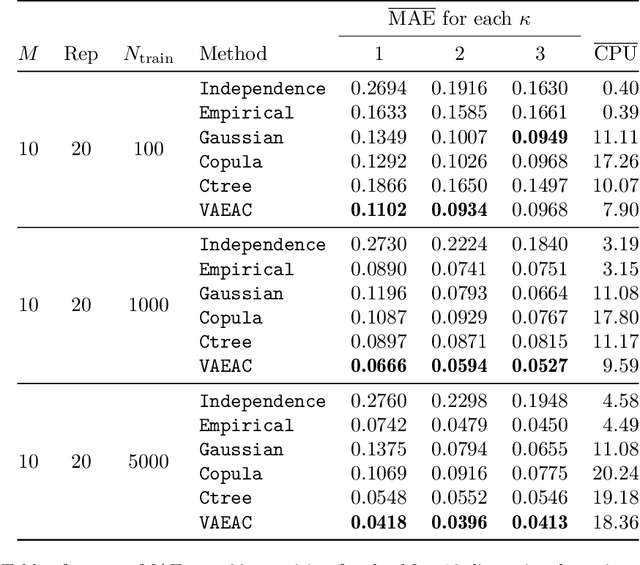
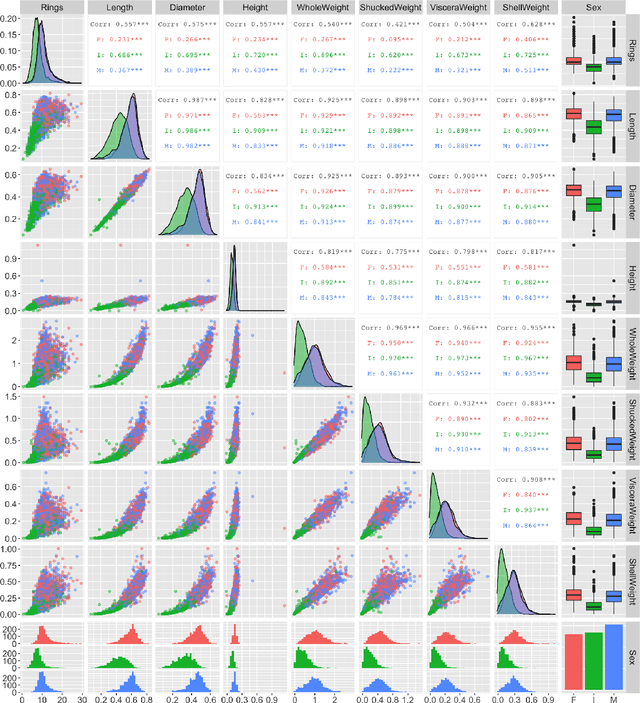
Shapley values are today extensively used as a model-agnostic explanation framework to explain complex predictive machine learning models. Shapley values have desirable theoretical properties and a sound mathematical foundation. Precise Shapley value estimates for dependent data rely on accurate modeling of the dependencies between all feature combinations. In this paper, we use a variational autoencoder with arbitrary conditioning (VAEAC) to model all feature dependencies simultaneously. We demonstrate through comprehensive simulation studies that VAEAC outperforms the state-of-the-art methods for a wide range of settings for both continuous and mixed dependent features. Finally, we apply VAEAC to the Abalone data set from the UCI Machine Learning Repository.