Similarity Equivariant Linear Transformation of Joint Orientation-Scale Space Representations

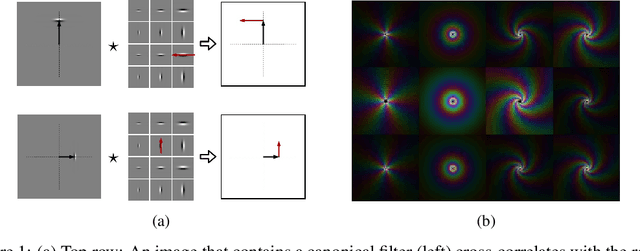
Convolution is conventionally defined as a linear operation on functions of one or more variables which commutes with shifts. Group convolution generalizes the concept to linear operations on functions of group elements representing more general geometric transformations and which commute with those transformations. Since similarity transformation is the most general geometric transformation on images that preserves shape, the group convolution that is equivariant to similarity transformation is the most general shape preserving linear operator. Because similarity transformations have four free parameters, group convolutions are defined on four-dimensional, joint orientation-scale spaces. Although prior work on equivariant linear operators has been limited to discrete groups, the similarity group is continuous. In this paper, we describe linear operators on discrete representations that are equivariant to continuous similarity transformation. This is achieved by using a basis of functions that is it joint shiftable-twistable-scalable. These pinwheel functions use Fourier series in the orientation dimension and Laplace transform in the log-scale dimension to form a basis of spatially localized functions that can be continuously interpolated in position, orientation and scale. Although this result is potentially significant with respect to visual computation generally, we present an initial demonstration of its utility by using it to compute a shape equivariant distribution of closed contours traced by particles undergoing Brownian motion in velocity. The contours are constrained by sets of points and line endings representing well known bistable illusory contour inducing patterns.

Euclidean Invariant Recognition of 2D Shapes Using Histograms of Magnitudes of Local Fourier-Mellin Descriptors

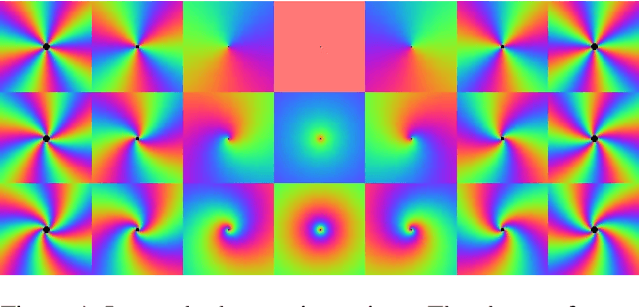
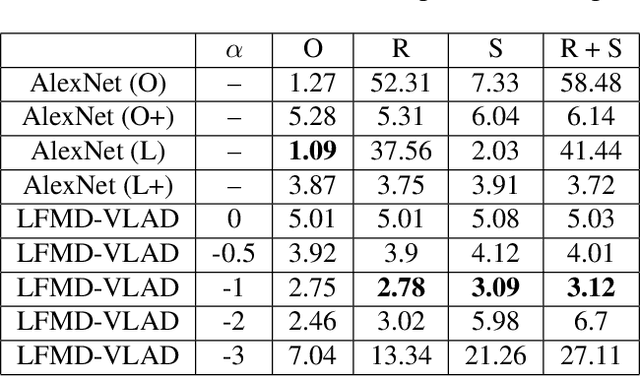
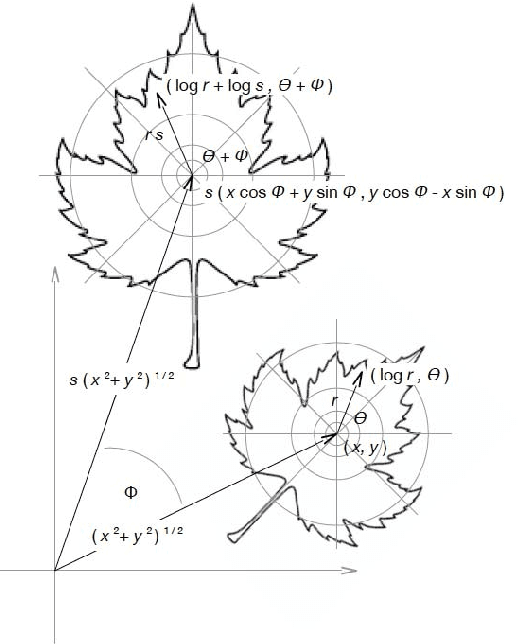
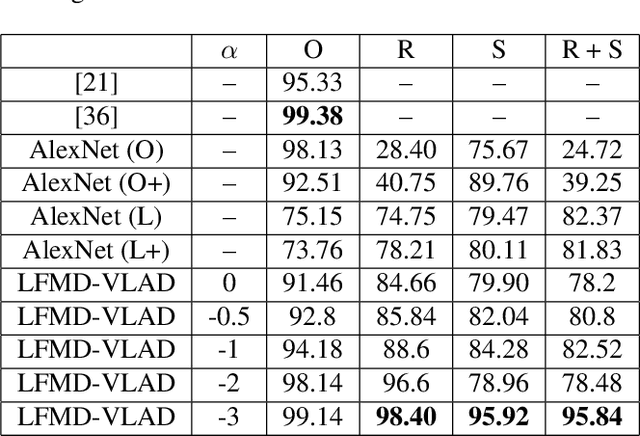
Because the magnitude of inner products with its basis functions are invariant to rotation and scale change, the Fourier-Mellin transform has long been used as a component in Euclidean invariant 2D shape recognition systems. Yet Fourier-Mellin transform magnitudes are only invariant to rotation and scale changes about a known center point, and full Euclidean invariant shape recognition is not possible except when this center point can be consistently and accurately identified. In this paper, we describe a system where a Fourier-Mellin transform is computed at every point in the image. The spatial support of the Fourier-Mellin basis functions is made local by multiplying them with a polynomial envelope. Significantly, the magnitudes of convolutions with these complex filters at isolated points are not (by themselves) used as features for Euclidean invariant shape recognition because reliable discrimination would require filters with spatial support large enough to fully encompass the shapes. Instead, we rely on the fact that normalized histograms of magnitudes are fully Euclidean invariant. We demonstrate a system based on the VLAD machine learning method that performs Euclidean invariant recognition of 2D shapes and requires an order of magnitude less training data than comparable methods based on convolutional neural networks.

Increased Complexity and Fitness of Artificial Cells that Reproduce Using Spatially Distributed Asynchronous Parallel Processes

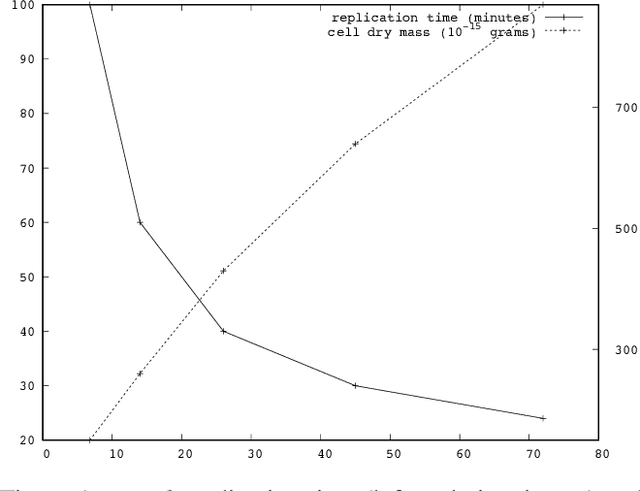
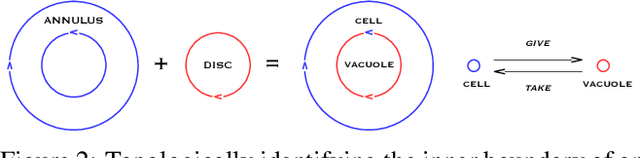
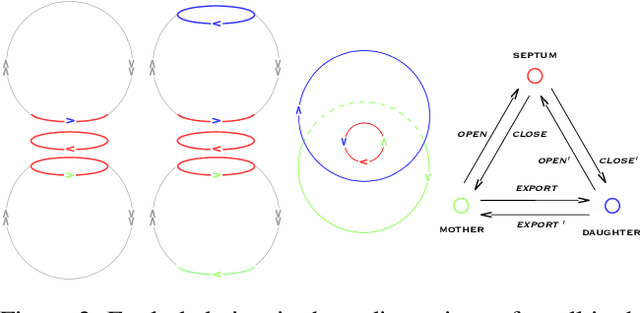
Replication time is among the most important components of a bacterial cell's reproductive fitness. Paradoxically, larger cells replicate in less time than smaller cells despite the fact that building a larger cell requires increased quantities of raw materials and energy. This feat is primarily accomplished by the massive over expression of ribosomes, which permits translation of mRNA into protein, the limiting step in reproduction, to occur at a scale that would be impossible were it not for the use of parallel processing. In computer science, spatial parallelism is the distribution of work across the nodes of a distributed-memory multicomputer system. Despite the fact that a non-negligible fraction of artificial life research is grounded in formulations based on spatially parallel substrates, there have been no examples of artificial organisms that use spatial parallelism to replicate in less time than smaller organisms. This paper describes artificial cells defined using a combinator-based artificial chemistry that replicate in less time than smaller cells. This is achieved by employing extra copies of programs implementing the limiting steps in the process used by the cells to synthesize their component parts. Significant speedup is demonstrated, despite the increased complexity of control and export processes necessitated by the use of a parallel replication strategy.

Towards Complex Artificial Life

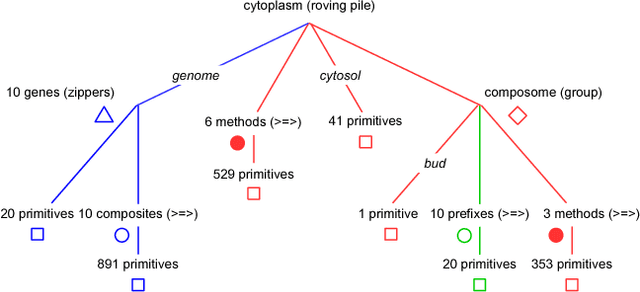
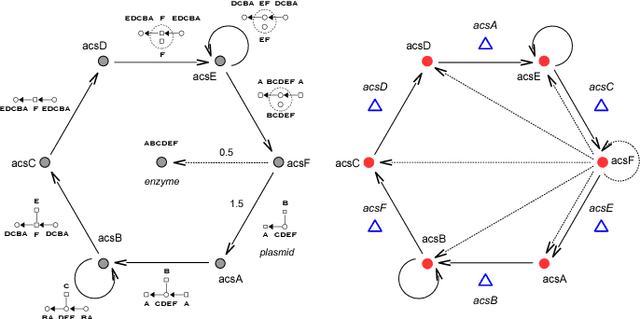
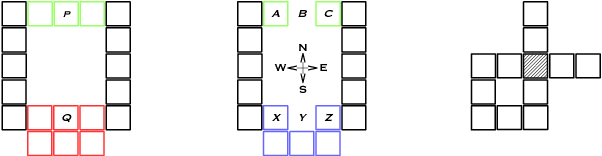
An object-oriented combinator chemistry was used to construct an artificial organism with a system architecture possessing characteristics necessary for organisms to evolve into more complex forms. This architecture supports modularity by providing a mechanism for the construction of executable modules called $methods$ that can be duplicated and specialized to increase complexity. At the same time, its support for concurrency provides the flexibility in execution order necessary for redundancy, degeneracy and parallelism to mitigate increased replication costs. The organism is a moving, self-replicating, spatially distributed assembly of elemental combinators called a $roving \: pile.$ The pile hosts an asynchronous message passing computation implemented by parallel subprocesses encoded by genes distributed through out the pile like the plasmids of a bacterial cell.

Programs as Polypeptides

We describe a visual programming language for defining behaviors manifested by reified actors in a 2D virtual world that can be compiled into programs comprised of sequences of combinators that are themselves reified as actors. This makes it possible to build programs that build programs from components of a few fixed types delivered by diffusion using processes that resemble chemistry as much as computation.