Euclidean Invariant Recognition of 2D Shapes Using Histograms of Magnitudes of Local Fourier-Mellin Descriptors

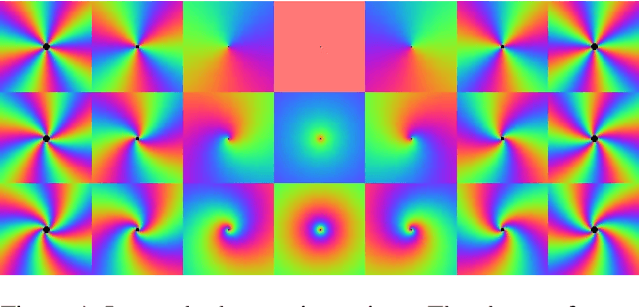
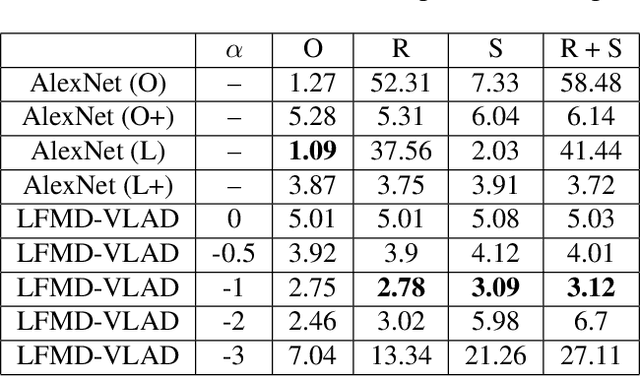
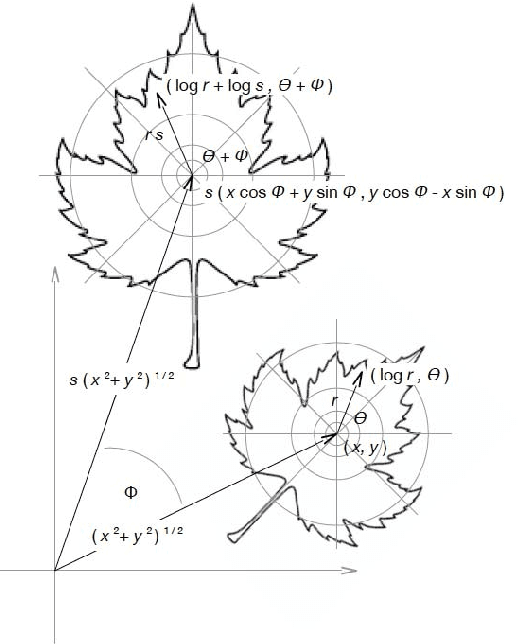
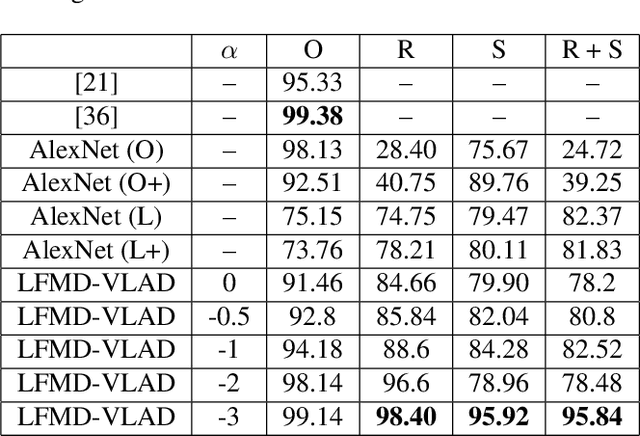
Because the magnitude of inner products with its basis functions are invariant to rotation and scale change, the Fourier-Mellin transform has long been used as a component in Euclidean invariant 2D shape recognition systems. Yet Fourier-Mellin transform magnitudes are only invariant to rotation and scale changes about a known center point, and full Euclidean invariant shape recognition is not possible except when this center point can be consistently and accurately identified. In this paper, we describe a system where a Fourier-Mellin transform is computed at every point in the image. The spatial support of the Fourier-Mellin basis functions is made local by multiplying them with a polynomial envelope. Significantly, the magnitudes of convolutions with these complex filters at isolated points are not (by themselves) used as features for Euclidean invariant shape recognition because reliable discrimination would require filters with spatial support large enough to fully encompass the shapes. Instead, we rely on the fact that normalized histograms of magnitudes are fully Euclidean invariant. We demonstrate a system based on the VLAD machine learning method that performs Euclidean invariant recognition of 2D shapes and requires an order of magnitude less training data than comparable methods based on convolutional neural networks.