Covariate balancing using the integral probability metric for causal inference

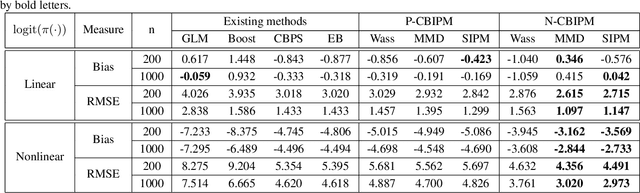
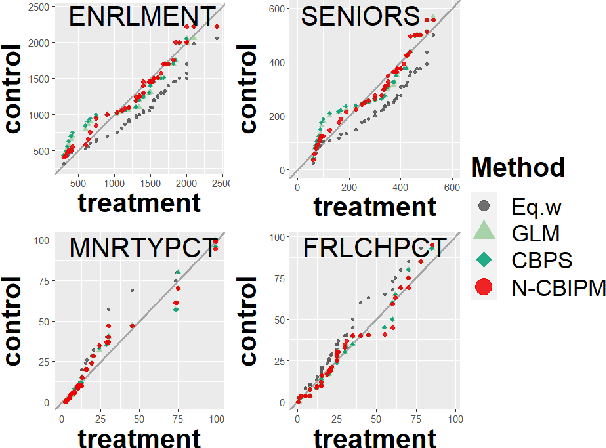
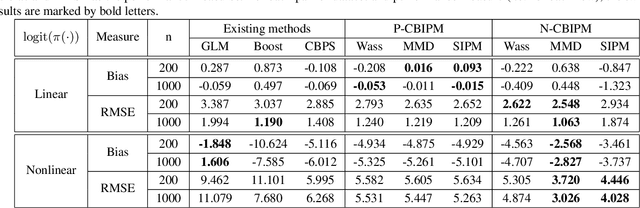
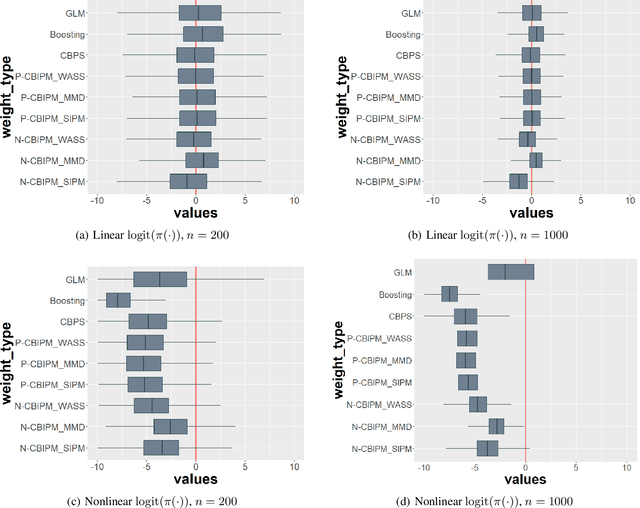
Weighting methods in causal inference have been widely used to achieve a desirable level of covariate balancing. However, the existing weighting methods have desirable theoretical properties only when a certain model, either the propensity score or outcome regression model, is correctly specified. In addition, the corresponding estimators do not behave well for finite samples due to large variance even when the model is correctly specified. In this paper, we consider to use the integral probability metric (IPM), which is a metric between two probability measures, for covariate balancing. Optimal weights are determined so that weighted empirical distributions for the treated and control groups have the smallest IPM value for a given set of discriminators. We prove that the corresponding estimator can be consistent without correctly specifying any model (neither the propensity score nor the outcome regression model). In addition, we empirically show that our proposed method outperforms existing weighting methods with large margins for finite samples.

Causal Rule Ensemble: Interpretable Inference of Heterogeneous Treatment Effects

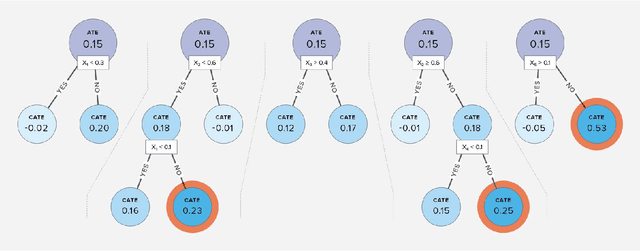
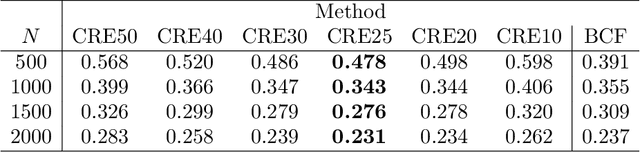
In environmental epidemiology, it is critically important to identify subpopulations that are most vulnerable to the adverse effects of air pollution so we can develop targeted interventions. In recent years, there have been many methodological developments for addressing heterogeneity of treatment effects in causal inference. A common approach is to estimate the conditional average treatment effect (CATE) for a pre-specified covariate set. However, this approach does not provide an easy-to-interpret tool for identifying susceptible subpopulations or discover new subpopulations that are not defined a priori by the researchers. In this paper, we propose a new causal rule ensemble (CRE) method with two features simultaneously: 1) ensuring interpretability by revealing heterogeneous treatment effect structures in terms of decision rules and 2) providing CATE estimates with high statistical precision similar to causal machine learning algorithms. We provide theoretical results that guarantee consistency of the estimated causal effects for the newly discovered causal rules. Furthermore, via simulations, we show that the CRE method has competitive performance on its ability to discover subpopulations and then accurately estimate the causal effects. We also develop a new sensitivity analysis method that examine robustness to unmeasured confounding bias. Lastly, we apply the CRE method to the study of the effects of long-term exposure to air pollution on the 5-year mortality rate of the New England Medicare-enrolled population in United States. Code is available at https://github.com/kwonsang/causal_rule_ensemble.