Sharp Inequalities between Total Variation and Hellinger Distances for Gaussian Mixtures

We study the relation between the total variation (TV) and Hellinger distances between two Gaussian location mixtures. Our first result establishes a general upper bound: for any two mixing distributions supported on a compact set, the Hellinger distance between the two mixtures is controlled by the TV distance raised to a power $1-o(1)$, where the $o(1)$ term is of order $1/\log\log(1/\mathrm{TV})$. We also construct two sequences of mixing distributions that demonstrate the sharpness of this bound. Taken together, our results resolve an open problem raised in Jia et al. (2023) and thus lead to an entropic characterization of learning Gaussian mixtures in total variation. Our inequality also yields optimal robust estimation of Gaussian mixtures in Hellinger distance, which has a direct implication for bounding the minimax regret of empirical Bayes under Huber contamination.

Covariate balancing using the integral probability metric for causal inference

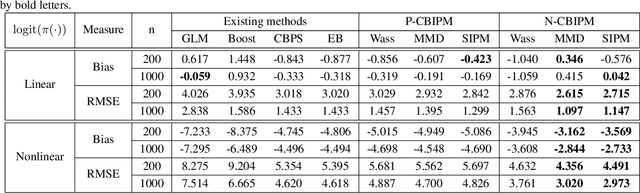
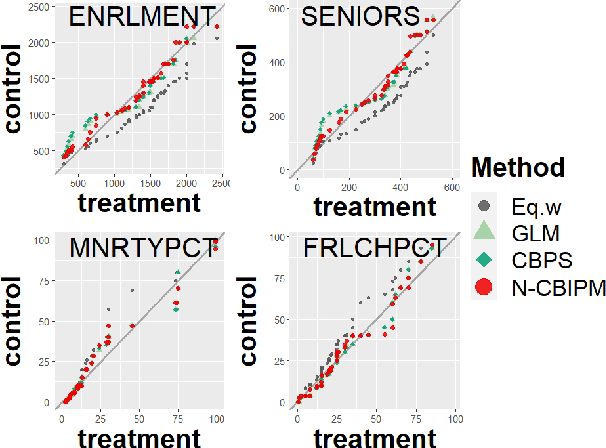
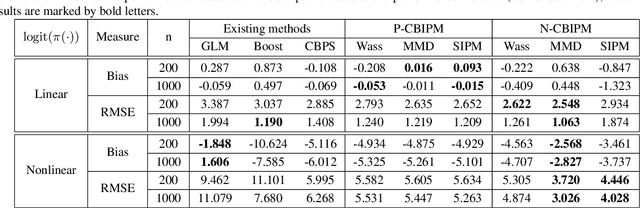
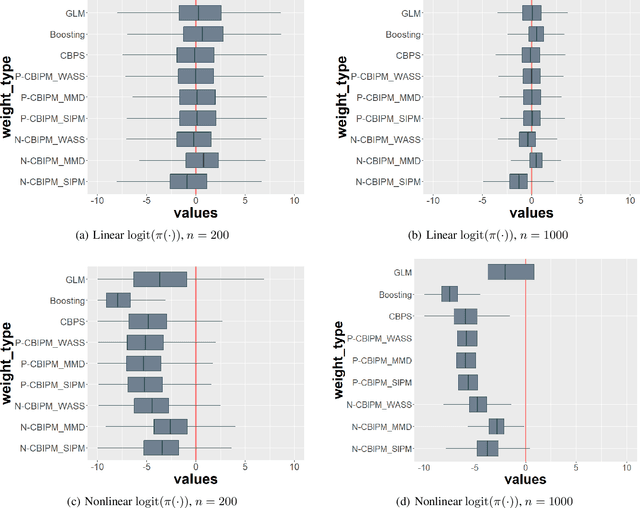
Weighting methods in causal inference have been widely used to achieve a desirable level of covariate balancing. However, the existing weighting methods have desirable theoretical properties only when a certain model, either the propensity score or outcome regression model, is correctly specified. In addition, the corresponding estimators do not behave well for finite samples due to large variance even when the model is correctly specified. In this paper, we consider to use the integral probability metric (IPM), which is a metric between two probability measures, for covariate balancing. Optimal weights are determined so that weighted empirical distributions for the treated and control groups have the smallest IPM value for a given set of discriminators. We prove that the corresponding estimator can be consistent without correctly specifying any model (neither the propensity score nor the outcome regression model). In addition, we empirically show that our proposed method outperforms existing weighting methods with large margins for finite samples.