Konstantinos K. Delibasis
Efficient UAV Coverage in Large Convex Quadrilateral Areas with Elliptical Footprints
Feb 18, 2025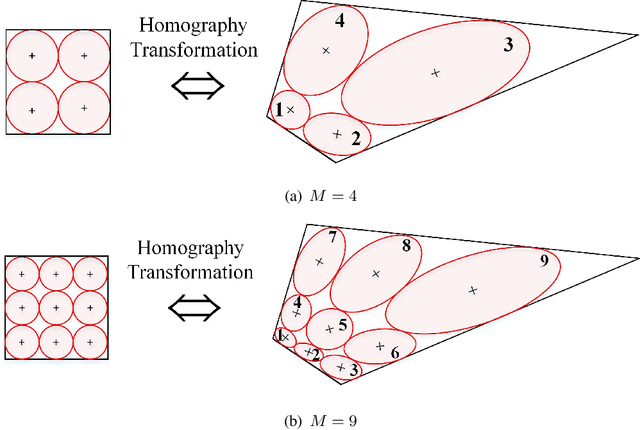
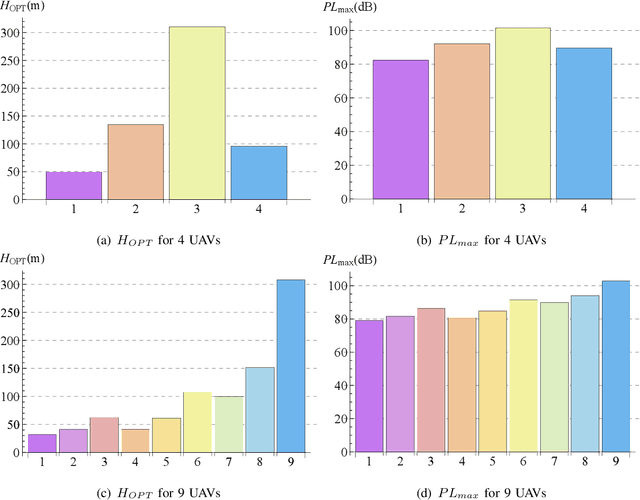
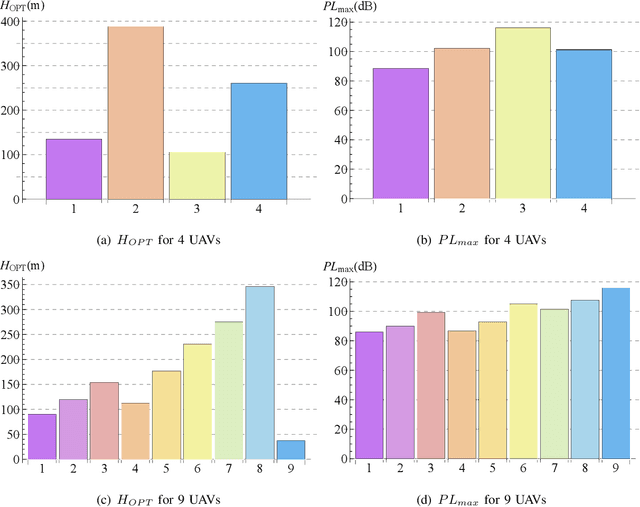
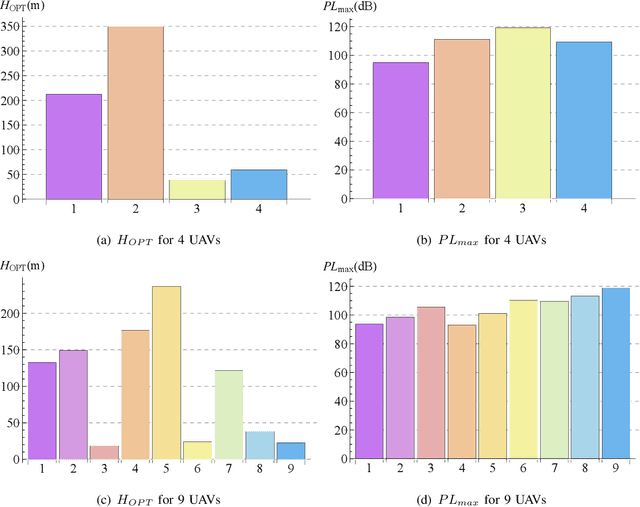
Abstract:Unmanned Aerial Vehicles (UAVs) have gained significant attention for improving wireless communication, especially in emergencies or as a complement to existing cellular infrastructure. This letter addresses the problem of efficiently covering a large convex quadrilateral using multiple UAVs, where each UAV generates elliptical coverage footprints based on its altitude and antenna tilt. The challenge is approached using circle-packing techniques within a unit square to arrange UAVs in an optimal configuration. Subsequently, a homography transformation is applied to map the unit square onto the quadrilateral area, ensuring that the UAVs' elliptical footprints cover the entire region. Numerical simulations demonstrate the effectiveness of the proposed method, providing insight into coverage density and optimal altitude configurations for different placement scenarios. The results highlight the scalability and potential for improving UAV-based communication systems, focusing on maximizing coverage efficiency in large areas with irregular shapes.
Hermite coordinate interpolation kernels: application to image zooming
Mar 19, 2024Abstract:A number of basic image processing tasks, such as any geometric transformation require interpolation at subpixel image values. In this work we utilize the multidimensional coordinate Hermite spline interpolation defined on non-equal spaced, rectilinear grids and apply it to a very common image processing task, image zooming. Since Hermite interpolation utilizes function values, as well as partial derivative values, it is natural to apply it to image processing tasks as a special case of equi-spaced grid, using numerical approximations of the image partial derivatives at each pixel. Furthermore, the task of image interpolation requires the calculation of image values at positions with nono-zero fractional part. Thus, any spline interpolation can be written as convolution with an appropriate kernel. In this context we generate the Hermite kernels according to the derived $n-$dimensional interpolant of Theorem 2 in [1]. We show that despite the increased complexity of the interpolant, once the kernels are constructed, the Hermite spline interpolation can be applied to images as efficiently as any other less complicated method. Finally, we perform illustrative numerical examples to showcase the applicability and high accuracy of the proposed Hermite kernels for image zooming, compared to other interpolation methods, both traditional convolution-based, as well as employing deep learning, in terms of PSNR, as well as SSIM error metrics. The proposed Hermite spline kernels outperform all other methods in the majority of the test images, in experiments using many cascaded repetitions of the zoom operation. Interesting conclusions can be drawn considering all methods under comparison.
On the Terminal Location Uncertainty in Elliptical Footprints: Application in Air-to-Ground Links
Sep 13, 2023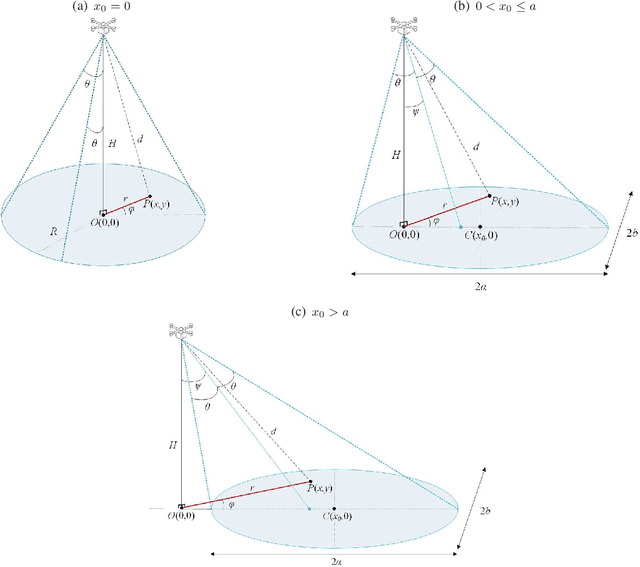
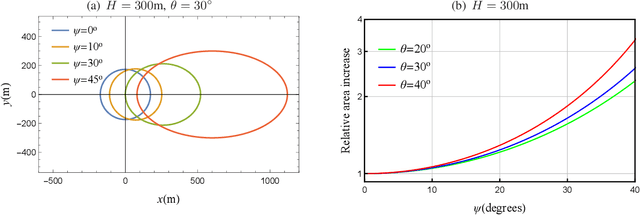
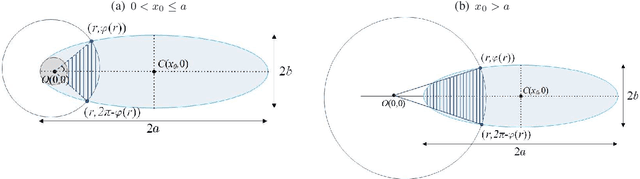
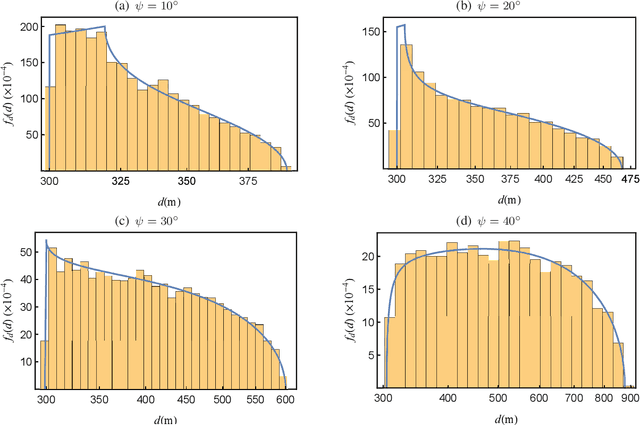
Abstract:Wireless transmitters (Txs) radiating directionally downwards often generate circular footprints on the ground. In certain scenarios, using elliptical cells can offer increased flexibility for providing user coverage, owing to the unique network characteristics. For instance, an elliptical footprint can be produced when a practical directional antenna with unequal azimuth and elevation half-power beamwidths is used in high-speed railway networks. Another common scenario involves the production of an elliptical footprint when an airborne Tx radiates at an angle by tilting its directional antenna by a few degrees. This paper aims to investigate, for the first time, the association between the random user location within an elliptical coverage area and the performance of a wireless communication link by considering these scenarios. We assume an unmanned aerial vehicle (UAV) as a Tx, although a tall cellular base station tower could also be employed without losing generality. To better understand the impact of random location, we derive relevant distance metrics and investigate the outage probability of the link for the two scenarios, taking both random terminal location and fading impairments into account. The findings may provide valuable insights into the performance of similar wireless systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge