Konstantinos A. Voulgaris
DeepMP for Non-Negative Sparse Decomposition
Jul 28, 2020
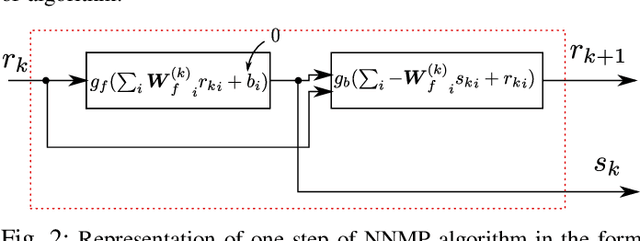
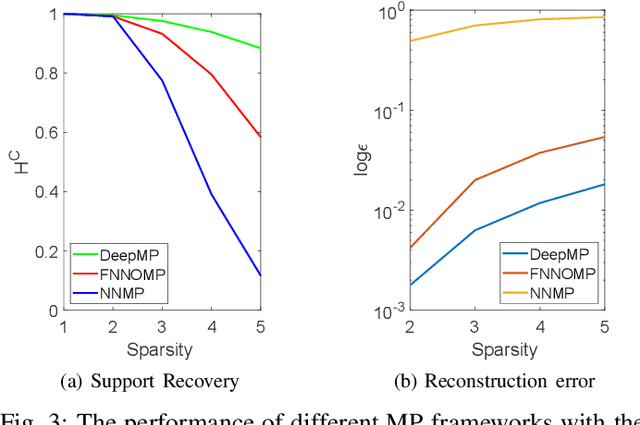
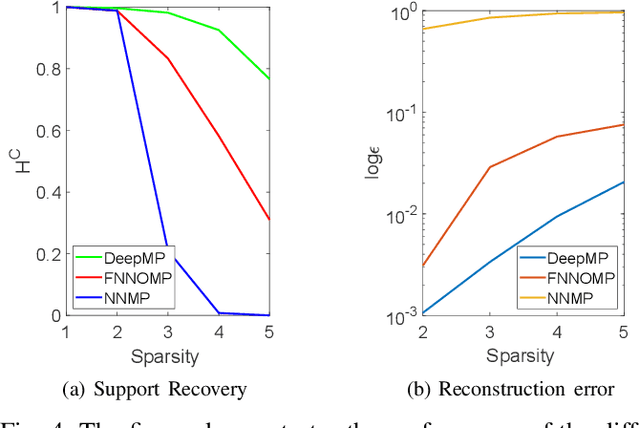
Abstract:Non-negative signals form an important class of sparse signals. Many algorithms have already beenproposed to recover such non-negative representations, where greedy and convex relaxed algorithms are among the most popular methods. The greedy techniques are low computational cost algorithms, which have also been modified to incorporate the non-negativity of the representations. One such modification has been proposed for Matching Pursuit (MP) based algorithms, which first chooses positive coefficients and uses a non-negative optimisation technique that guarantees the non-negativity of the coefficients. The performance of greedy algorithms, like all non-exhaustive search methods, suffer from high coherence with the linear generative model, called the dictionary. We here first reformulate the non-negative matching pursuit algorithm in the form of a deep neural network. We then show that the proposed model after training yields a significant improvement in terms of exact recovery performance, compared to other non-trained greedy algorithms, while keeping the complexity low.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge