Physics-Informed Deep Neural Network Method for Limited Observability State Estimation

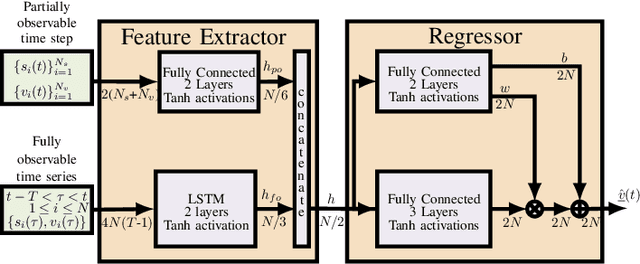
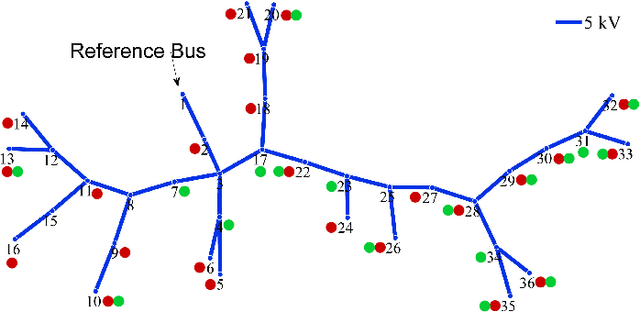
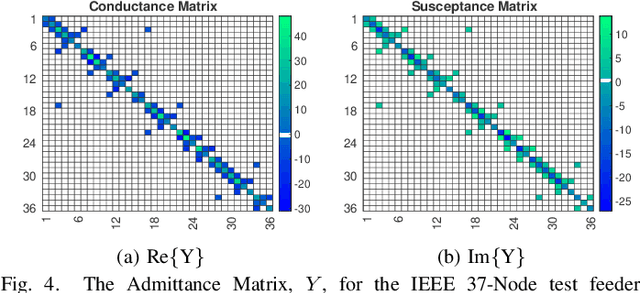
The precise knowledge regarding the state of the power grid is important in order to ensure optimal and reliable grid operation. Specifically, knowing the state of the distribution grid becomes increasingly important as more renewable energy sources are connected directly into the distribution network, increasing the fluctuations of the injected power. In this paper, we consider the case when the distribution grid becomes partially observable, and the state estimation problem is under-determined. We present a new methodology that leverages a deep neural network (DNN) to estimate the grid state. The standard DNN training method is modified to explicitly incorporate the physical information of the grid topology and line/shunt admittance. We show that our method leads to a superior accuracy of the estimation when compared to the case when no physical information is provided. Finally, we compare the performance of our method to the standard state estimation approach, which is based on the weighted least squares with pseudo-measurements, and show that our method performs significantly better with respect to the estimation accuracy.

Sacrificing Accuracy for Reduced Computation: Cascaded Inference Based on Softmax Confidence

We study the tradeoff between computational effort and accuracy in a cascade of deep neural networks. During inference, early termination in the cascade is controlled by confidence levels derived directly from the softmax outputs of intermediate classifiers. The advantage of early termination is that classification is performed using less computation, thus adjusting the computational effort to the complexity of the input. Moreover, dynamic modification of confidence thresholds allow one to trade accuracy for computational effort without requiring retraining. Basing of early termination on softmax classifier outputs is justified by experimentation that demonstrates an almost linear relation between confidence levels in intermediate classifiers and accuracy. Our experimentation with architectures based on ResNet obtained the following results. (i) A speedup of 1.5 that sacrifices 1.4% accuracy with respect to the CIFAR-10 test set. (ii) A speedup of 1.19 that sacrifices 0.7% accuracy with respect to the CIFAR-100 test set. (iii) A speedup of 2.16 that sacrifices 1.4% accuracy with respect to the SVHN test set.