Kirby Banman
Resonance in Weight Space: Covariate Shift Can Drive Divergence of SGD with Momentum
Mar 22, 2022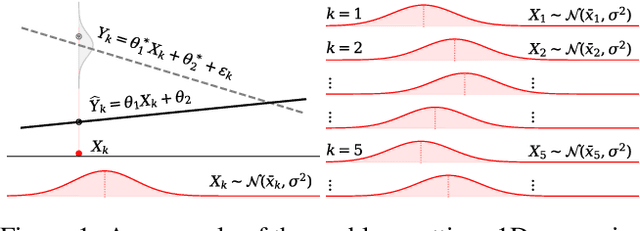
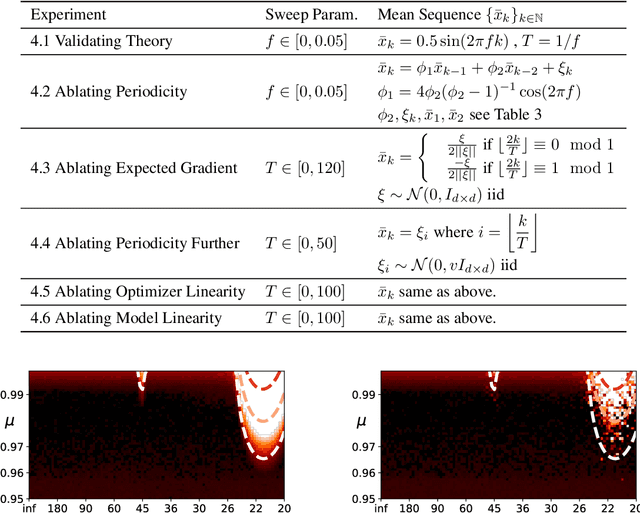
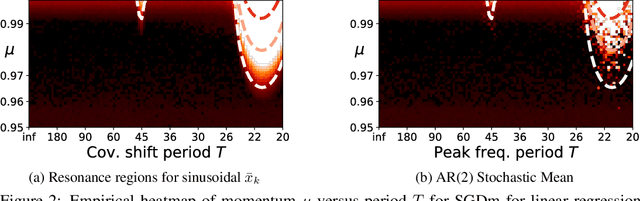

Abstract:Most convergence guarantees for stochastic gradient descent with momentum (SGDm) rely on iid sampling. Yet, SGDm is often used outside this regime, in settings with temporally correlated input samples such as continual learning and reinforcement learning. Existing work has shown that SGDm with a decaying step-size can converge under Markovian temporal correlation. In this work, we show that SGDm under covariate shift with a fixed step-size can be unstable and diverge. In particular, we show SGDm under covariate shift is a parametric oscillator, and so can suffer from a phenomenon known as resonance. We approximate the learning system as a time varying system of ordinary differential equations, and leverage existing theory to characterize the system's divergence/convergence as resonant/nonresonant modes. The theoretical result is limited to the linear setting with periodic covariate shift, so we empirically supplement this result to show that resonance phenomena persist even under non-periodic covariate shift, nonlinear dynamics with neural networks, and optimizers other than SGDm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge