Deformable Butterfly: A Highly Structured and Sparse Linear Transform

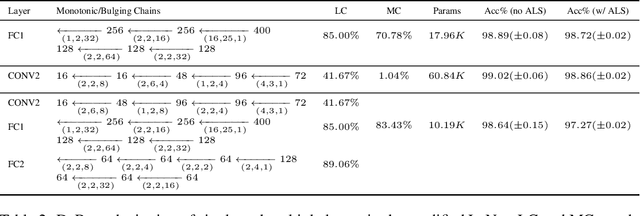
We introduce a new kind of linear transform named Deformable Butterfly (DeBut) that generalizes the conventional butterfly matrices and can be adapted to various input-output dimensions. It inherits the fine-to-coarse-grained learnable hierarchy of traditional butterflies and when deployed to neural networks, the prominent structures and sparsity in a DeBut layer constitutes a new way for network compression. We apply DeBut as a drop-in replacement of standard fully connected and convolutional layers, and demonstrate its superiority in homogenizing a neural network and rendering it favorable properties such as light weight and low inference complexity, without compromising accuracy. The natural complexity-accuracy tradeoff arising from the myriad deformations of a DeBut layer also opens up new rooms for analytical and practical research. The codes and Appendix are publicly available at: https://github.com/ruilin0212/DeBut.

EZCrop: Energy-Zoned Channels for Robust Output Pruning

Recent results have revealed an interesting observation in a trained convolutional neural network (CNN), namely, the rank of a feature map channel matrix remains surprisingly constant despite the input images. This has led to an effective rank-based channel pruning algorithm, yet the constant rank phenomenon remains mysterious and unexplained. This work aims at demystifying and interpreting such rank behavior from a frequency-domain perspective, which as a bonus suggests an extremely efficient Fast Fourier Transform (FFT)-based metric for measuring channel importance without explicitly computing its rank. We achieve remarkable CNN channel pruning based on this analytically sound and computationally efficient metric and adopt it for repetitive pruning to demonstrate robustness via our scheme named Energy-Zoned Channels for Robust Output Pruning (EZCrop), which shows consistently better results than other state-of-the-art channel pruning methods.