Kevin Stehle
On the Difficulty of Designing Processor Arrays for Deep Neural Networks
Jun 24, 2020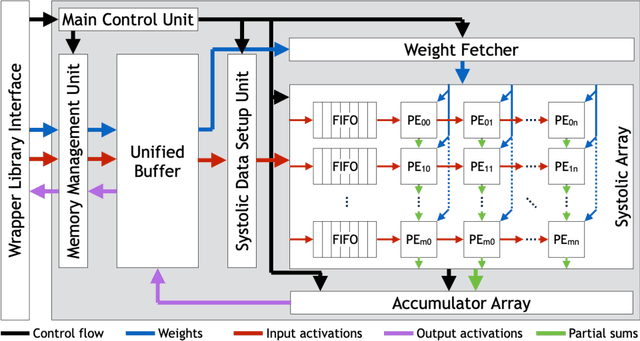
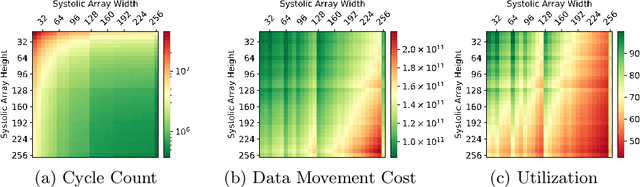
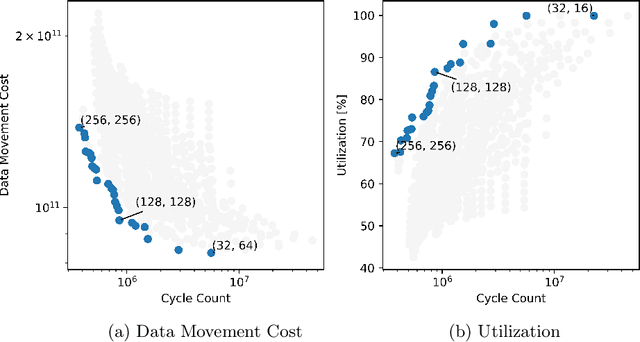
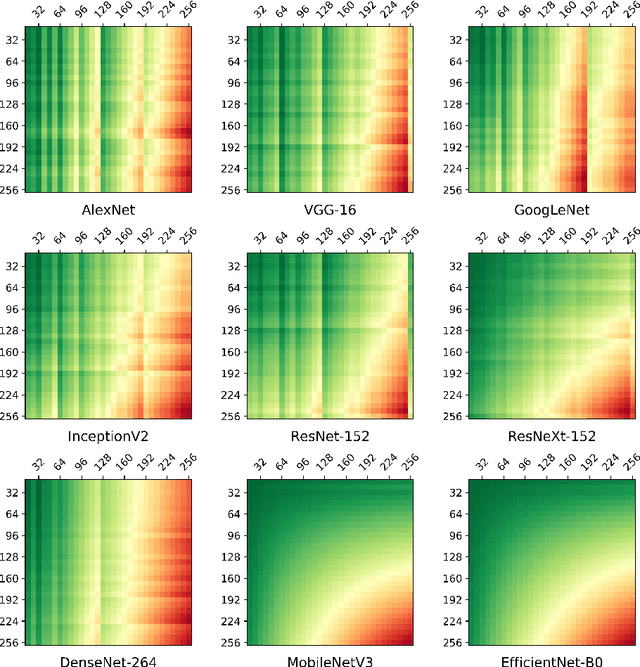
Abstract:Systolic arrays are a promising computing concept which is in particular inline with CMOS technology trends and linear algebra operations found in the processing of artificial neural networks. The recent success of such deep learning methods in a wide set of applications has led to a variety of models, which albeit conceptual similar as based on convolutions and fully-connected layers, in detail show a huge diversity in operations due to a large design space: An operand's dimension varies substantially since it depends on design principles such as receptive field size, number of features, striding, dilating and grouping of features. Last, recent networks extent previously plain feedforward models by various connectivity, such as in ResNet or DenseNet. The problem of choosing an optimal systolic array configuration cannot be solved analytically, thus instead methods and tools are required that facilitate a fast and accurate reasoning about optimality in terms of total cycles, utilization, and amount of data movements. In this work we introduce Camuy, a lightweight model of a weight-stationary systolic array for linear algebra operations that allows quick explorations of different configurations, such as systolic array dimensions and input/output bitwidths. Camuy aids accelerator designers in either finding optimal configurations for a particular network architecture or for robust performance across a variety of network architectures. It offers simple integration into existing machine learning tool stacks (e.g TensorFlow) through custom operators. We present an analysis of popular DNN models to illustrate how it can estimate required cycles, data movement costs, as well as systolic array utilization, and show how the progress in network architecture design impacts the efficiency of inference on accelerators based on systolic arrays.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge