Feature anomaly detection system (FADS) for intelligent manufacturing

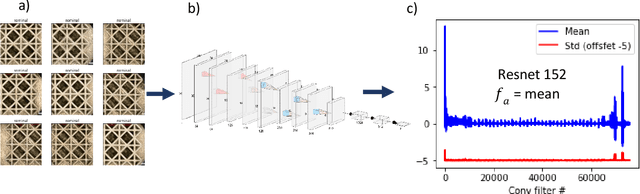
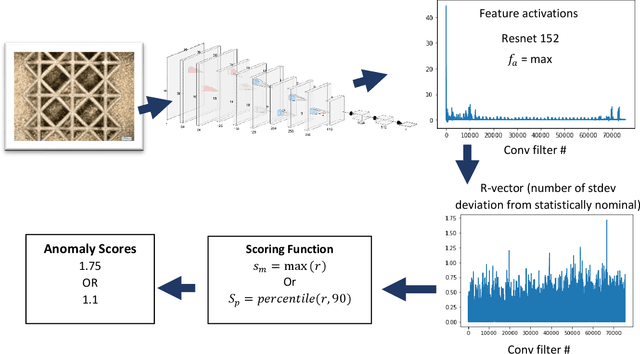
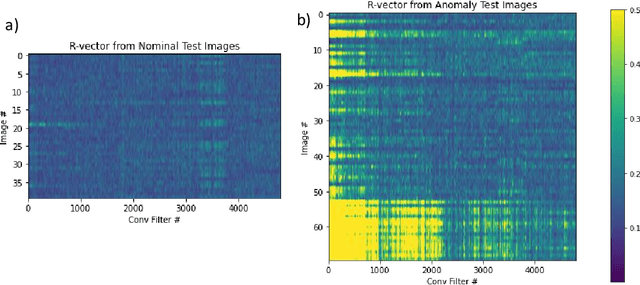
Anomaly detection is important for industrial automation and part quality assurance, and while humans can easily detect anomalies in components given a few examples, designing a generic automated system that can perform at human or above human capabilities remains a challenge. In this work, we present a simple new anomaly detection algorithm called FADS (feature-based anomaly detection system) which leverages pretrained convolutional neural networks (CNN) to generate a statistical model of nominal inputs by observing the activation of the convolutional filters. During inference the system compares the convolutional filter activation of the new input to the statistical model and flags activations that are outside the expected range of values and therefore likely an anomaly. By using a pretrained network, FADS demonstrates excellent performance similar to or better than other machine learning approaches to anomaly detection while at the same time FADS requires no tuning of the CNN weights. We demonstrate FADS ability by detecting process parameter changes on a custom dataset of additively manufactured lattices. The FADS localization algorithm shows that textural differences that are visible on the surface can be used to detect process parameter changes. In addition, we test FADS on benchmark datasets, such as the MVTec Anomaly Detection dataset, and report good results.

Enabling Nonlinear Manifold Projection Reduced-Order Models by Extending Convolutional Neural Networks to Unstructured Data

We propose a nonlinear manifold learning technique based on deep autoencoders that is appropriate for model order reduction of physical systems in complex geometries. Convolutional neural networks have proven to be highly advantageous for systems demonstrating a slow-decaying Kolmogorov n-width. However, these networks are restricted to data on structured meshes. Unstructured meshes are often required for performing analyses of real systems with complex geometry. Our custom graph convolution operators based on the available differential operators for a given spatial discretization effectively extend the application space of these deep autoencoders to systems with arbitrarily complex geometry that can only be efficiently discretized using unstructured meshes. We propose sets of convolution operators based on the spatial derivative operators for the underlying spatial discretization, making the method particularly well suited to data arising from the solution of partial differential equations. We demonstrate the method using examples from heat transfer and fluid mechanics and show better than an order of magnitude improvement in accuracy over linear subspace methods.