On the development of a practical Bayesian optimisation algorithm for expensive experiments and simulations with changing environmental conditions

Experiments in engineering are typically conducted in controlled environments where parameters can be set to any desired value. This assumes that the same applies in a real-world setting -- an assumption that is often incorrect as many experiments are influenced by uncontrollable environmental conditions such as temperature, humidity and wind speed. When optimising such experiments, the focus should lie on finding optimal values conditionally on these uncontrollable variables. This article extends Bayesian optimisation to the optimisation of systems in changing environments that include controllable and uncontrollable parameters. The extension fits a global surrogate model over all controllable and environmental variables but optimises only the controllable parameters conditional on measurements of the uncontrollable variables. The method is validated on two synthetic test functions and the effects of the noise level, the number of the environmental parameters, the parameter fluctuation, the variability of the uncontrollable parameters, and the effective domain size are investigated. ENVBO, the proposed algorithm resulting from this investigation, is applied to a wind farm simulator with eight controllable and one environmental parameter. ENVBO finds solutions for the full domain of the environmental variable that outperforms results from optimisation algorithms that only focus on a fixed environmental value in all but one case while using a fraction of their evaluation budget. This makes the proposed approach very sample-efficient and cost-effective. An off-the-shelf open-source version of ENVBO is available via the NUBO Python package.

On the development of a Bayesian optimisation framework for complex unknown systems

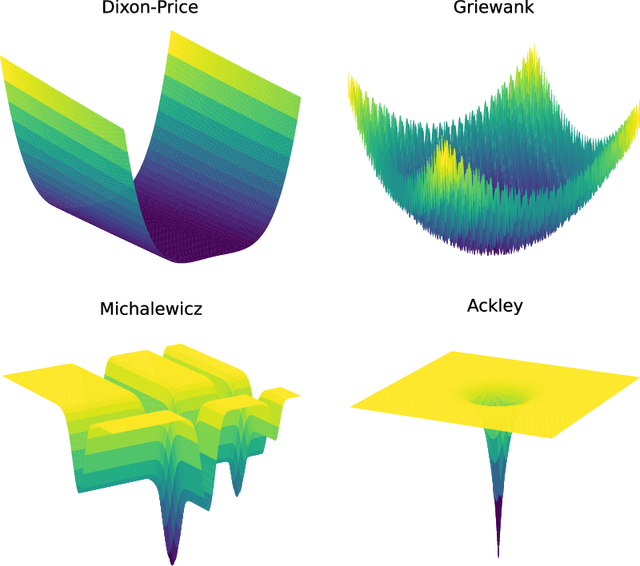
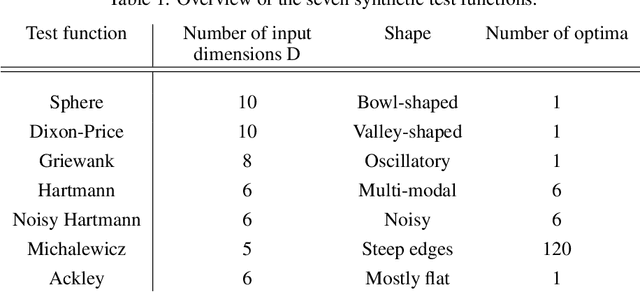
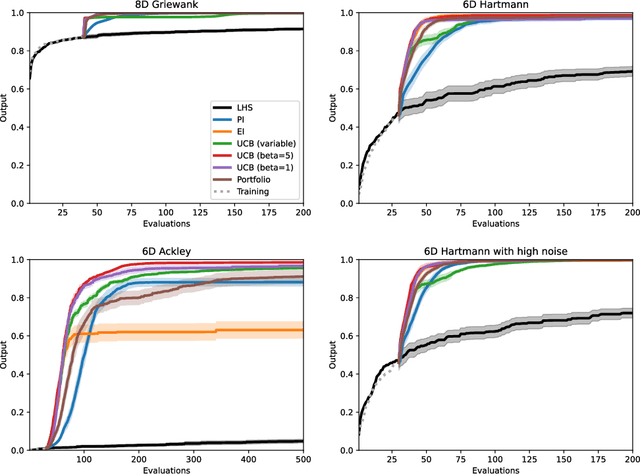
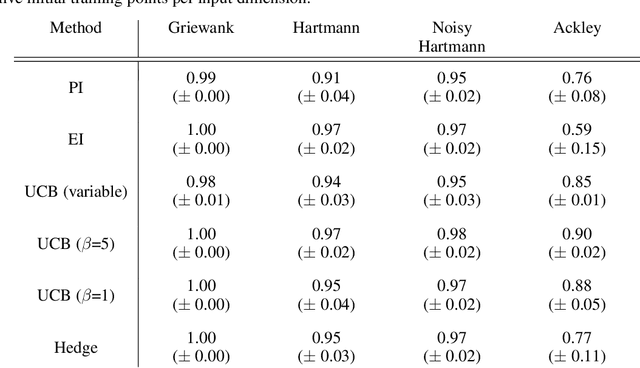
Bayesian optimisation provides an effective method to optimise expensive black box functions. It has recently been applied to problems in fluid dynamics. This paper studies and compares common Bayesian optimisation algorithms empirically on a range of synthetic test functions. It investigates the choice of acquisition function and number of training samples, exact calculation of acquisition functions and Monte Carlo based approaches and both single-point and multi-point optimisation. The test functions considered cover a wide selection of challenges and therefore serve as an ideal test bed to understand the performance of Bayesian optimisation and to identify general situations where Bayesian optimisation performs well and poorly. This knowledge can be utilised in applications, including those in fluid dynamics, where objective functions are unknown. The results of this investigation show that the choices to be made are less relevant for relatively simple functions, while optimistic acquisition functions such as Upper Confidence Bound should be preferred for more complex objective functions. Furthermore, results from the Monte Carlo approach are comparable to results from analytical acquisition functions. In instances where the objective function allows parallel evaluations, the multi-point approach offers a quicker alternative, yet it may potentially require more objective function evaluations.