On the development of a Bayesian optimisation framework for complex unknown systems

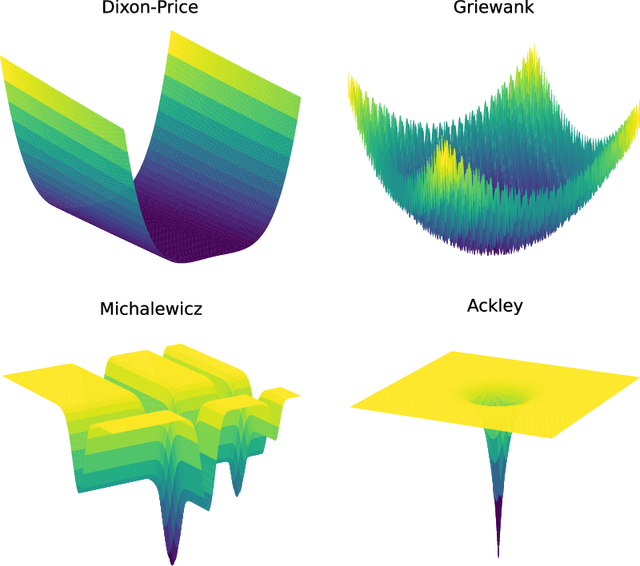
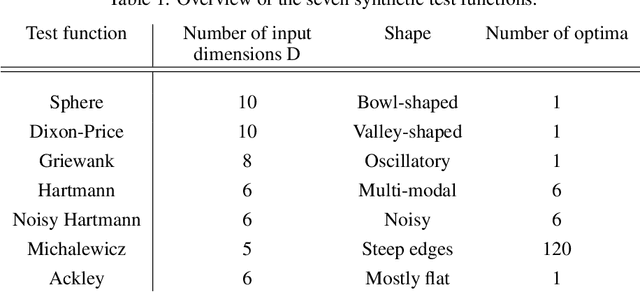
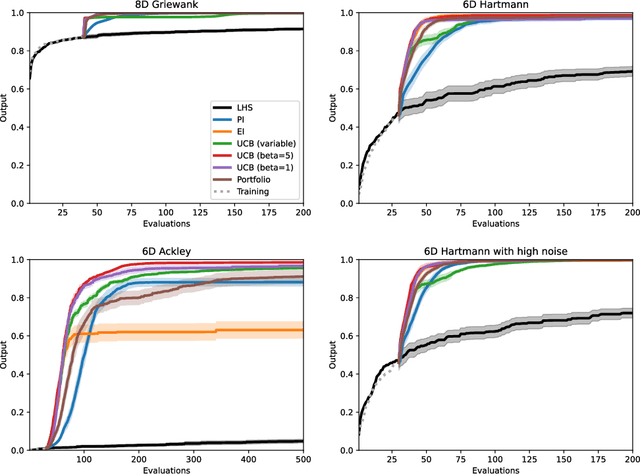
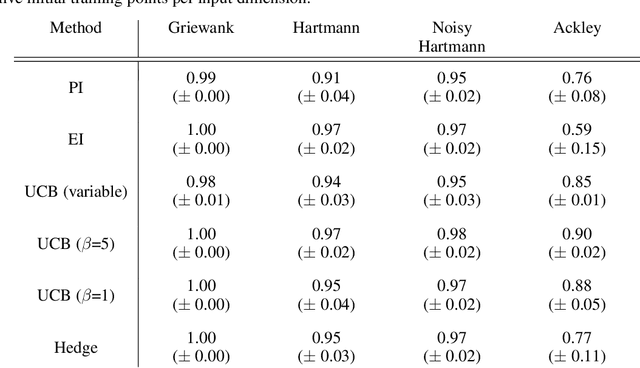
Bayesian optimisation provides an effective method to optimise expensive black box functions. It has recently been applied to problems in fluid dynamics. This paper studies and compares common Bayesian optimisation algorithms empirically on a range of synthetic test functions. It investigates the choice of acquisition function and number of training samples, exact calculation of acquisition functions and Monte Carlo based approaches and both single-point and multi-point optimisation. The test functions considered cover a wide selection of challenges and therefore serve as an ideal test bed to understand the performance of Bayesian optimisation and to identify general situations where Bayesian optimisation performs well and poorly. This knowledge can be utilised in applications, including those in fluid dynamics, where objective functions are unknown. The results of this investigation show that the choices to be made are less relevant for relatively simple functions, while optimistic acquisition functions such as Upper Confidence Bound should be preferred for more complex objective functions. Furthermore, results from the Monte Carlo approach are comparable to results from analytical acquisition functions. In instances where the objective function allows parallel evaluations, the multi-point approach offers a quicker alternative, yet it may potentially require more objective function evaluations.