Valid inference after prediction

Recent work has focused on the very common practice of prediction-based inference: that is, (i) using a pre-trained machine learning model to predict an unobserved response variable, and then (ii) conducting inference on the association between that predicted response and some covariates. As pointed out by Wang et al. [2020], applying a standard inferential approach in (ii) does not accurately quantify the association between the unobserved (as opposed to the predicted) response and the covariates. In recent work, Wang et al. [2020] and Angelopoulos et al. [2023] propose corrections to step (ii) in order to enable valid inference on the association between the unobserved response and the covariates. Here, we show that the method proposed by Angelopoulos et al. [2023] successfully controls the type 1 error rate and provides confidence intervals with correct nominal coverage, regardless of the quality of the pre-trained machine learning model used to predict the unobserved response. However, the method proposed by Wang et al. [2020] provides valid inference only under very strong conditions that rarely hold in practice: for instance, if the machine learning model perfectly approximates the true regression function in the study population of interest.

Generalized Data Thinning Using Sufficient Statistics

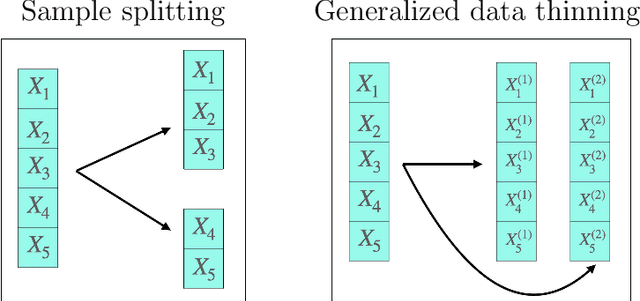
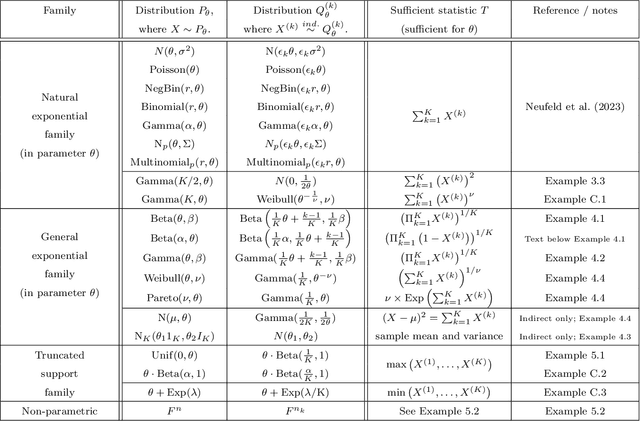
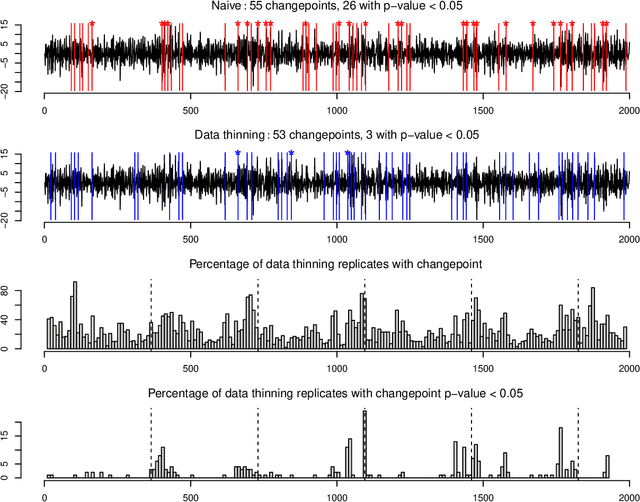
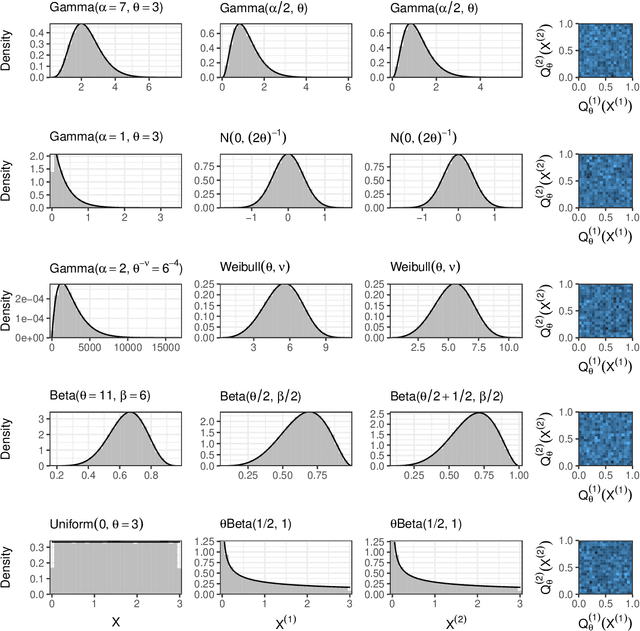
Our goal is to develop a general strategy to decompose a random variable $X$ into multiple independent random variables, without sacrificing any information about unknown parameters. A recent paper showed that for some well-known natural exponential families, $X$ can be "thinned" into independent random variables $X^{(1)}, \ldots, X^{(K)}$, such that $X = \sum_{k=1}^K X^{(k)}$. In this paper, we generalize their procedure by relaxing this summation requirement and simply asking that some known function of the independent random variables exactly reconstruct $X$. This generalization of the procedure serves two purposes. First, it greatly expands the families of distributions for which thinning can be performed. Second, it unifies sample splitting and data thinning, which on the surface seem to be very different, as applications of the same principle. This shared principle is sufficiency. We use this insight to perform generalized thinning operations for a diverse set of families.