Decomposing Gaussians with Unknown Covariance

Common workflows in machine learning and statistics rely on the ability to partition the information in a data set into independent portions. Recent work has shown that this may be possible even when conventional sample splitting is not (e.g., when the number of samples $n=1$, or when observations are not independent and identically distributed). However, the approaches that are currently available to decompose multivariate Gaussian data require knowledge of the covariance matrix. In many important problems (such as in spatial or longitudinal data analysis, and graphical modeling), the covariance matrix may be unknown and even of primary interest. Thus, in this work we develop new approaches to decompose Gaussians with unknown covariance. First, we present a general algorithm that encompasses all previous decomposition approaches for Gaussian data as special cases, and can further handle the case of an unknown covariance. It yields a new and more flexible alternative to sample splitting when $n>1$. When $n=1$, we prove that it is impossible to partition the information in a multivariate Gaussian into independent portions without knowing the covariance matrix. Thus, we use the general algorithm to decompose a single multivariate Gaussian with unknown covariance into dependent parts with tractable conditional distributions, and demonstrate their use for inference and validation. The proposed decomposition strategy extends naturally to Gaussian processes. In simulation and on electroencephalography data, we apply these decompositions to the tasks of model selection and post-selection inference in settings where alternative strategies are unavailable.

Generalized Data Thinning Using Sufficient Statistics

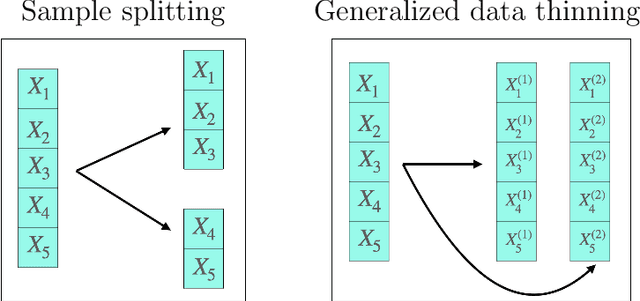
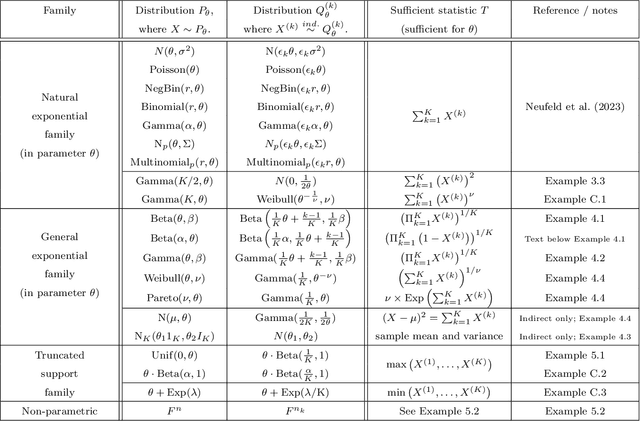
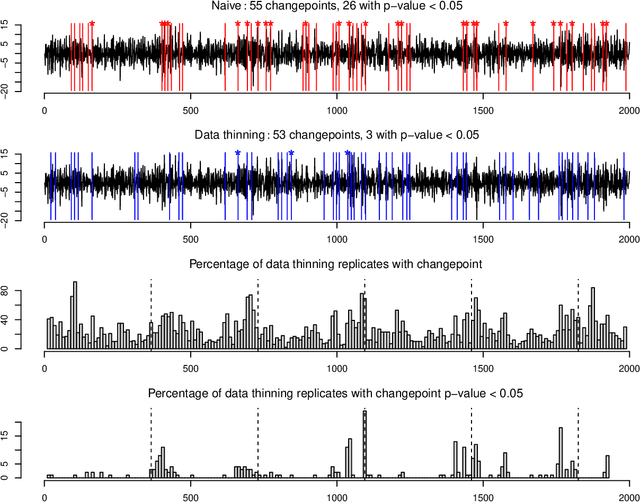
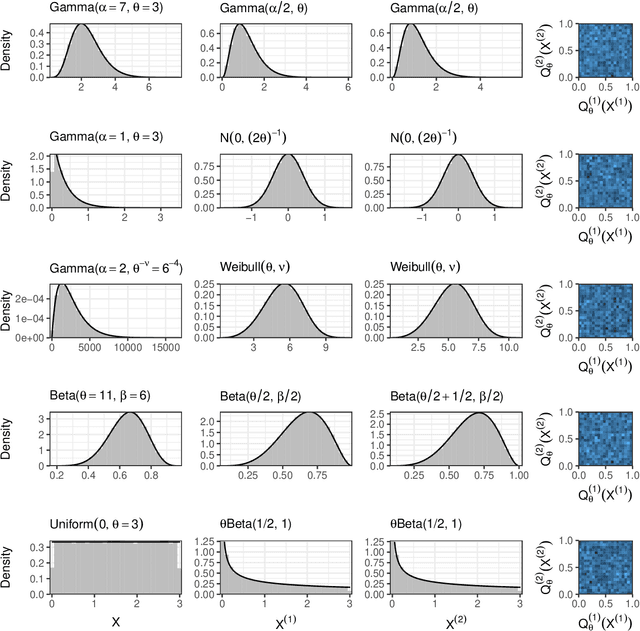
Our goal is to develop a general strategy to decompose a random variable $X$ into multiple independent random variables, without sacrificing any information about unknown parameters. A recent paper showed that for some well-known natural exponential families, $X$ can be "thinned" into independent random variables $X^{(1)}, \ldots, X^{(K)}$, such that $X = \sum_{k=1}^K X^{(k)}$. In this paper, we generalize their procedure by relaxing this summation requirement and simply asking that some known function of the independent random variables exactly reconstruct $X$. This generalization of the procedure serves two purposes. First, it greatly expands the families of distributions for which thinning can be performed. Second, it unifies sample splitting and data thinning, which on the surface seem to be very different, as applications of the same principle. This shared principle is sufficiency. We use this insight to perform generalized thinning operations for a diverse set of families.

Data thinning for convolution-closed distributions

We propose data thinning, a new approach for splitting an observation into two or more independent parts that sum to the original observation, and that follow the same distribution as the original observation, up to a (known) scaling of a parameter. This proposal is very general, and can be applied to any observation drawn from a "convolution closed" distribution, a class that includes the Gaussian, Poisson, negative binomial, Gamma, and binomial distributions, among others. It is similar in spirit to -- but distinct from, and more easily applicable than -- a recent proposal known as data fission. Data thinning has a number of applications to model selection, evaluation, and inference. For instance, cross-validation via data thinning provides an attractive alternative to the "usual" approach of cross-validation via sample splitting, especially in unsupervised settings in which the latter is not applicable. In simulations and in an application to single-cell RNA-sequencing data, we show that data thinning can be used to validate the results of unsupervised learning approaches, such as k-means clustering and principal components analysis.