Generalization Analysis on Learning with a Concurrent Verifier

Machine learning technologies have been used in a wide range of practical systems. In practical situations, it is natural to expect the input-output pairs of a machine learning model to satisfy some requirements. However, it is difficult to obtain a model that satisfies requirements by just learning from examples. A simple solution is to add a module that checks whether the input-output pairs meet the requirements and then modifies the model's outputs. Such a module, which we call a {\em concurrent verifier} (CV), can give a certification, although how the generalizability of the machine learning model changes using a CV is unclear. This paper gives a generalization analysis of learning with a CV. We analyze how the learnability of a machine learning model changes with a CV and show a condition where we can obtain a guaranteed hypothesis using a verifier only in the inference time. We also show that typical error bounds based on Rademacher complexity will be no larger than that of the original model when using a CV in multi-class classification and structured prediction settings.

Differentiable Equilibrium Computation with Decision Diagrams for Stackelberg Models of Combinatorial Congestion Games

We address Stackelberg models of combinatorial congestion games (CCGs); we aim to optimize the parameters of CCGs so that the selfish behavior of non-atomic players attains desirable equilibria. This model is essential for designing such social infrastructures as traffic and communication networks. Nevertheless, computational approaches to the model have not been thoroughly studied due to two difficulties: (I) bilevel-programming structures and (II) the combinatorial nature of CCGs. We tackle them by carefully combining (I) the idea of \textit{differentiable} optimization and (II) data structures called \textit{zero-suppressed binary decision diagrams} (ZDDs), which can compactly represent sets of combinatorial strategies. Our algorithm numerically approximates the equilibria of CCGs, which we can differentiate with respect to parameters of CCGs by automatic differentiation. With the resulting derivatives, we can apply gradient-based methods to Stackelberg models of CCGs. Our method is tailored to induce Nesterov's acceleration and can fully utilize the empirical compactness of ZDDs. These technical advantages enable us to deal with CCGs with a vast number of combinatorial strategies. Experiments on real-world network design instances demonstrate the practicality of our method.

Variable Shift SDD: A More Succinct Sentential Decision Diagram

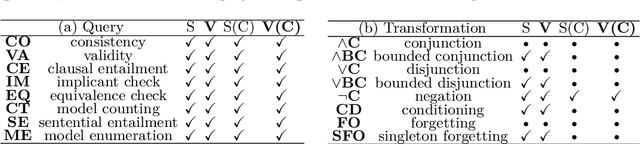
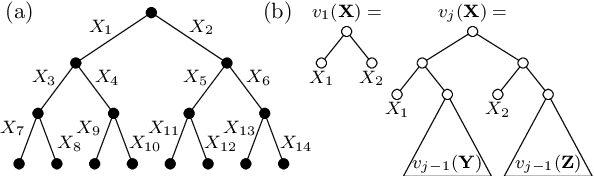
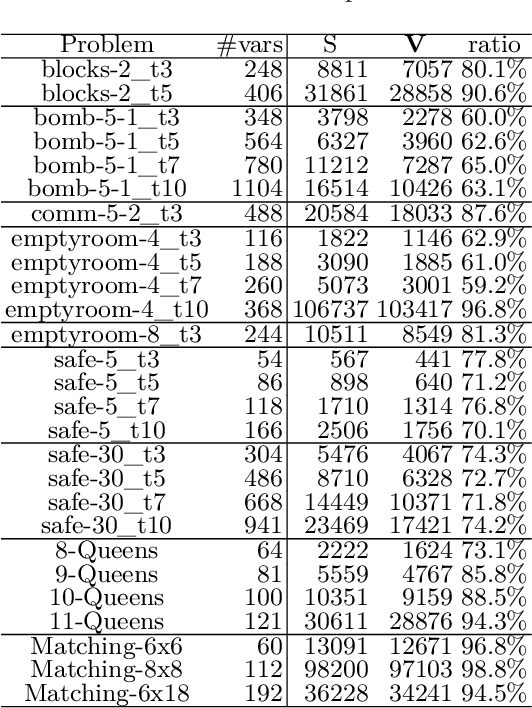
The Sentential Decision Diagram (SDD) is a tractable representation of Boolean functions that subsumes the famous Ordered Binary Decision Diagram (OBDD) as a strict subset. SDDs are attracting much attention because they are more succinct than OBDDs, as well as having canonical forms and supporting many useful queries and transformations such as model counting and Apply operation. In this paper, we propose a more succinct variant of SDD named Variable Shift SDD (VS-SDD). The key idea is to create a unique representation for Boolean functions that are equivalent under a specific variable substitution. We show that VS-SDDs are never larger than SDDs and there are cases in which the size of a VS-SDD is exponentially smaller than that of an SDD. Moreover, despite such succinctness, we show that numerous basic operations that are supported in polytime with SDD are also supported in polytime with VS-SDD. Experiments confirm that VS-SDDs are significantly more succinct than SDDs when applied to classical planning instances, where inherent symmetry exists.