Feature-level Malware Obfuscation in Deep Learning

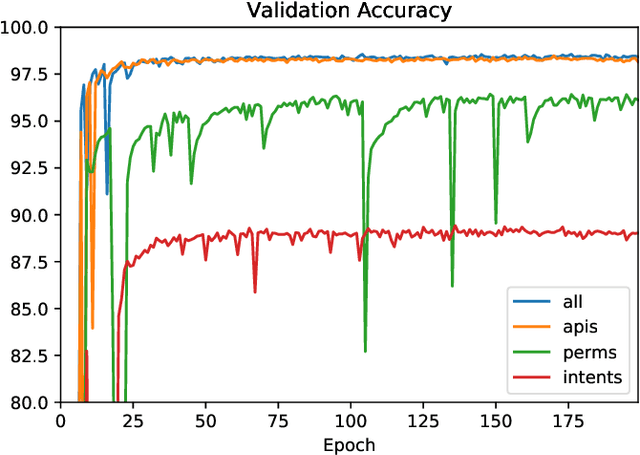
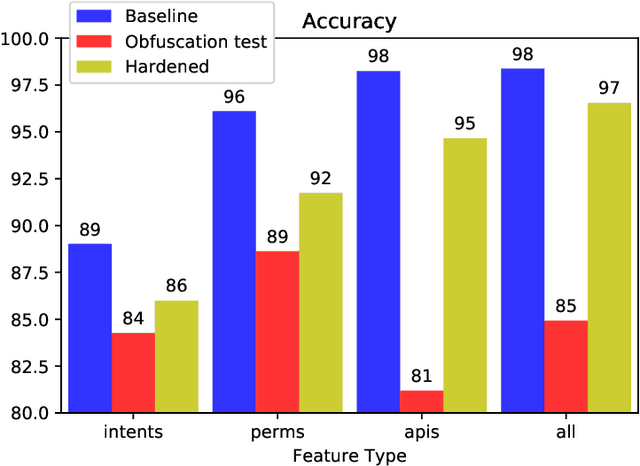
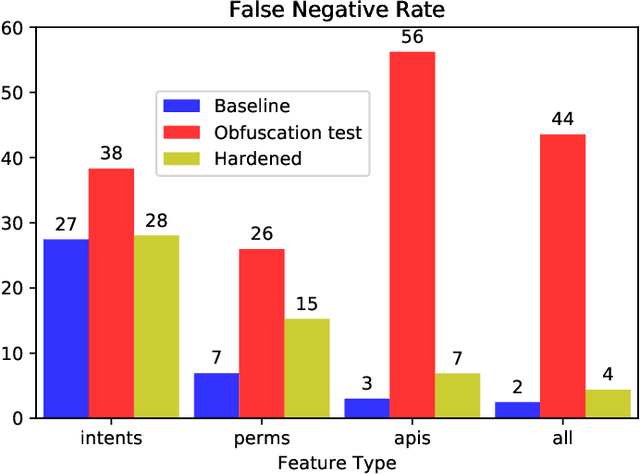
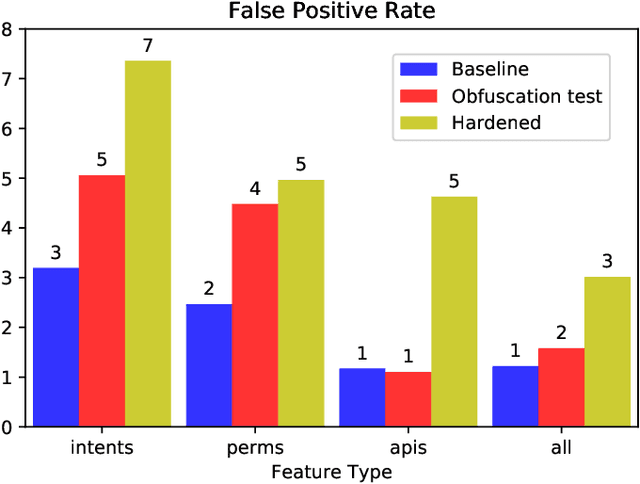
We consider the problem of detecting malware with deep learning models, where the malware may be combined with significant amounts of benign code. Examples of this include piggybacking and trojan horse attacks on a system, where malicious behavior is hidden within a useful application. Such added flexibility in augmenting the malware enables significantly more code obfuscation. Hence we focus on the use of static features, particularly Intents, Permissions, and API calls, which we presume cannot be ultimately hidden from the Android system, but only augmented with yet more such features. We first train a deep neural network classifier for malware classification using features of benign and malware samples. Then we demonstrate a steep increase in false negative rate (i.e., attacks succeed), simply by randomly adding features of a benign app to malware. Finally we test the use of data augmentation to harden the classifier against such attacks. We find that for API calls, it is possible to reject the vast majority of attacks, where using Intents or Permissions is less successful.

Clustering Gaussian Graphical Models

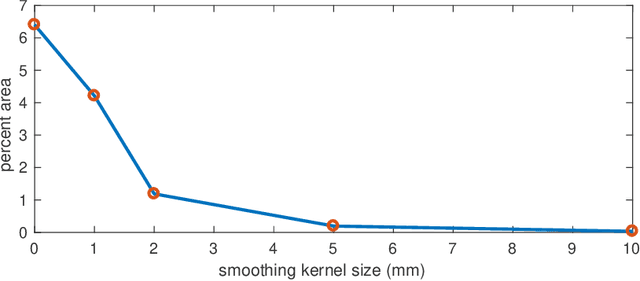
We derive an efficient method to perform clustering of nodes in Gaussian graphical models directly from sample data. Nodes are clustered based on the similarity of their network neighborhoods, with edge weights defined by partial correlations. In the limited-data scenario, where the covariance matrix would be rank-deficient, we are able to make use of matrix factors, and never need to estimate the actual covariance or precision matrix. We demonstrate the method on functional MRI data from the Human Connectome Project. A matlab implementation of the algorithm is provided.

On the Computation and Applications of Large Dense Partial Correlation Networks

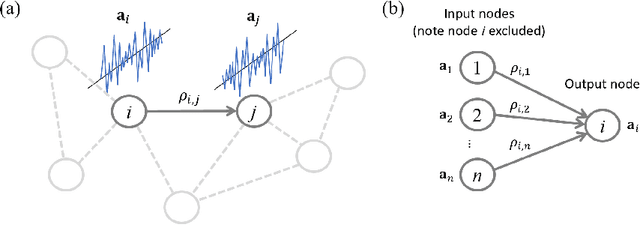
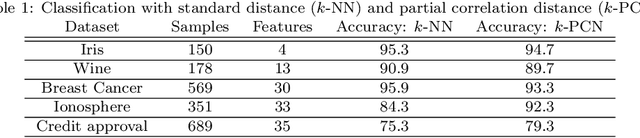
While sparse inverse covariance matrices are very popular for modeling network connectivity, the value of the dense solution is often overlooked. In fact the L2-regularized solution has deep connections to a number of important applications to spectral graph theory, dimensionality reduction, and uncertainty quantification. We derive an approach to directly compute the partial correlations based on concepts from inverse problem theory. This approach also leads to new insights on open problems such as model selection and data preprocessing, as well as new approaches which relate the above application areas.

Imaging with Rays: Microscopy, Medical Imaging, and Computer Vision

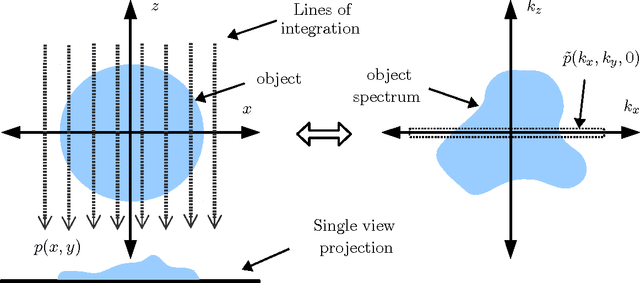
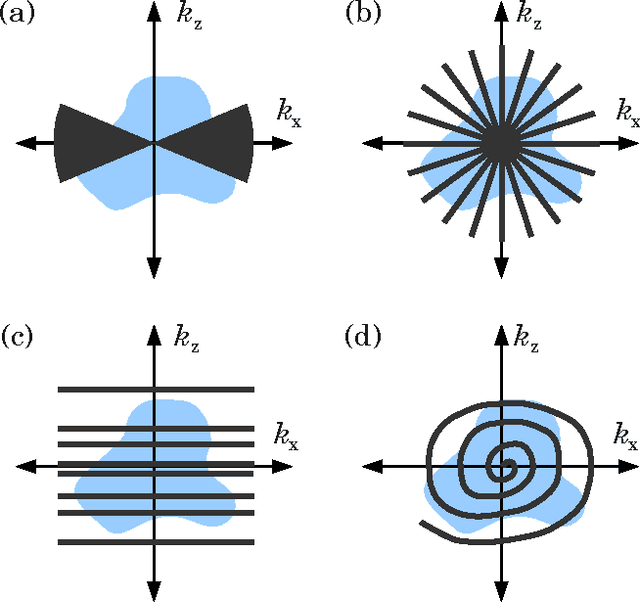
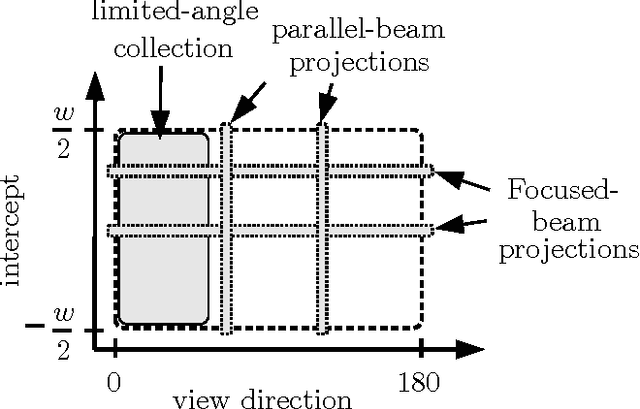
In this paper we broadly consider techniques which utilize projections on rays for data collection, with particular emphasis on optical techniques. We formulate a variety of imaging techniques as either special cases or extensions of tomographic reconstruction. We then consider how the techniques must be extended to describe objects containing occlusion, as with a self-occluding opaque object. We formulate the reconstruction problem as a regularized nonlinear optimization problem to simultaneously solve for object brightness and attenuation, where the attenuation can become infinite. We demonstrate various simulated examples for imaging opaque objects, including sparse point sources, a conventional multiview reconstruction technique, and a super-resolving technique which exploits occlusion to resolve an image.