Resampling Benchmark for Efficient Comprehensive Evaluation of Large Vision-Language Models

We propose an efficient evaluation protocol for large vision-language models (VLMs). Given their broad knowledge and reasoning capabilities, multiple benchmarks are needed for comprehensive assessment, making evaluation computationally expensive. To improve efficiency, we construct a subset that yields results comparable to full benchmark evaluations. Our benchmark classification experiments reveal that no single benchmark fully covers all challenges. We then introduce a subset construction method using farthest point sampling (FPS). Our experiments show that FPS-based benchmarks maintain a strong correlation (> 0.96) with full evaluations while using only ~1\% of the data. Additionally, applying FPS to an existing benchmark improves correlation with overall evaluation results, suggesting its potential to reduce unintended dataset biases.

Locally Self-Adjustive Smoothing for Measurement Noise Reduction with Application to Automated Peak Detection

Smoothing is widely used approach for measurement noise reduction in spectral analysis. However, it suffers from signal distortion caused by peak suppression. A locally self-adjustive smoothing method is developed that retains sharp peaks and less distort signals. The proposed method uses only one parameter that determines global smoothness, while balancing the local smoothness using data itself. Simulation and real experiments in comparison with existing convolution-based smoothing methods indicate both qualitatively and quantitatively improved noise reduction performance in practical scenarios. We also discuss parameter selection and demonstrate an application for the automated smoothing and detection of a given number of peaks from noisy measurement data.

Rethinking PointNet Embedding for Faster and Compact Model

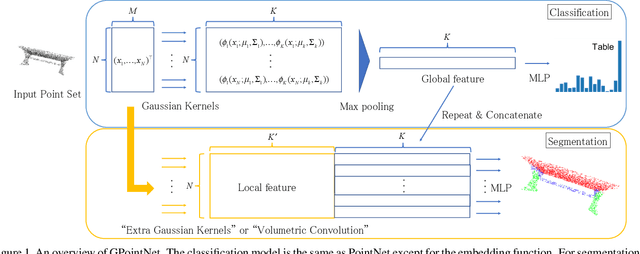
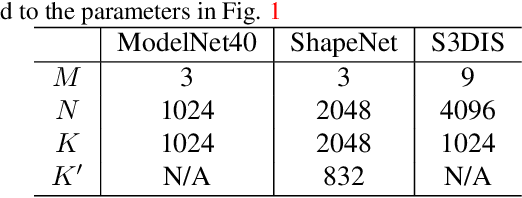
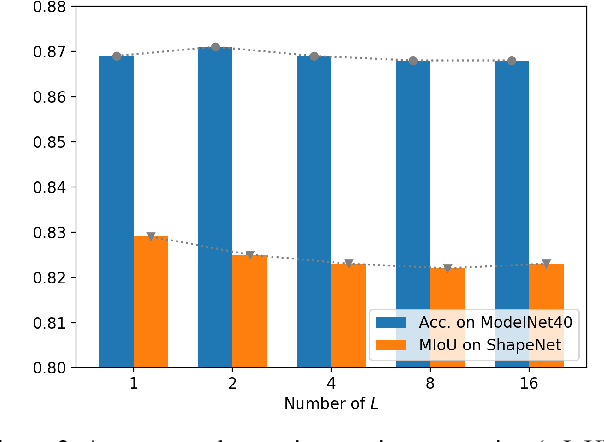
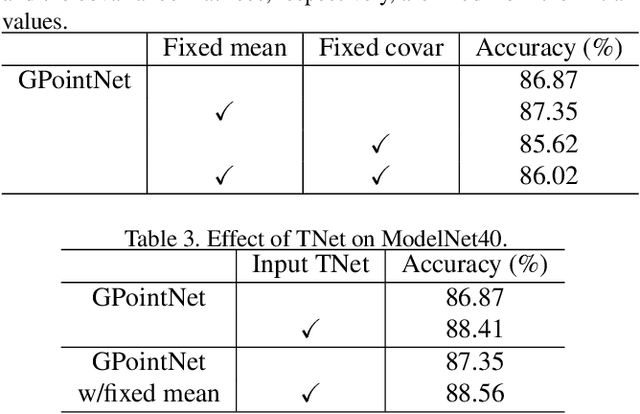
PointNet, which is the widely used point-wise embedding method and known as a universal approximator for continuous set functions, can process one million points per second. Nevertheless, real-time inference for the recent development of high-performing sensors is still challenging with existing neural network-based methods, including PointNet. In ordinary cases, the embedding function of PointNet behaves like a soft-indicator function that is activated when the input points exist in a certain local region of the input space. Leveraging this property, we reduce the computational costs of point-wise embedding by replacing the embedding function of PointNet with the soft-indicator function by Gaussian kernels. Moreover, we show that the Gaussian kernels also satisfy the universal approximation theorem that PointNet satisfies. In experiments, we verify that our model using the Gaussian kernels achieves comparable results to baseline methods, but with much fewer floating-point operations per sample up to 92\% reduction from PointNet.