Multiclass spectral feature scaling method for dimensionality reduction

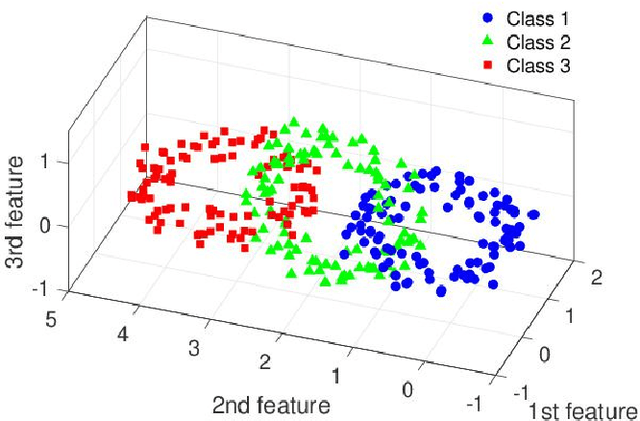
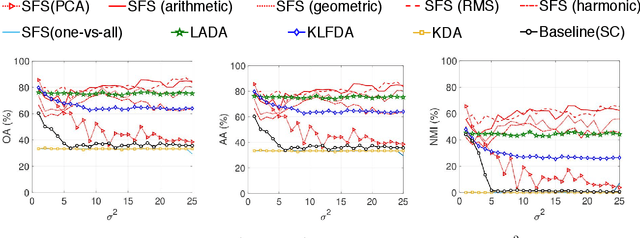
Irregular features disrupt the desired classification. In this paper, we consider aggressively modifying scales of features in the original space according to the label information to form well-separated clusters in low-dimensional space. The proposed method exploits spectral clustering to derive scaling factors that are used to modify the features. Specifically, we reformulate the Laplacian eigenproblem of the spectral clustering as an eigenproblem of a linear matrix pencil whose eigenvector has the scaling factors. Numerical experiments show that the proposed method outperforms well-established supervised dimensionality reduction methods for toy problems with more samples than features and real-world problems with more features than samples.

Spectral feature scaling method for supervised dimensionality reduction

Spectral dimensionality reduction methods enable linear separations of complex data with high-dimensional features in a reduced space. However, these methods do not always give the desired results due to irregularities or uncertainties of the data. Thus, we consider aggressively modifying the scales of the features to obtain the desired classification. Using prior knowledge on the labels of partial samples to specify the Fiedler vector, we formulate an eigenvalue problem of a linear matrix pencil whose eigenvector has the feature scaling factors. The resulting factors can modify the features of entire samples to form clusters in the reduced space, according to the known labels. In this study, we propose new dimensionality reduction methods supervised using the feature scaling associated with the spectral clustering. Numerical experiments show that the proposed methods outperform well-established supervised methods for toy problems with more samples than features, and are more robust regarding clustering than existing methods. Also, the proposed methods outperform existing methods regarding classification for real-world problems with more features than samples of gene expression profiles of cancer diseases. Furthermore, the feature scaling tends to improve the clustering and classification accuracies of existing unsupervised methods, as the proportion of training data increases.