Minimum Norm Method for Linear and Planar Sparse Arrays

Coprime and nested arrays are sparse arrays with enhanced degrees of freedom, which can be exploited in direction of arrival estimation using algorithms such as product processing, min processing, and MUSIC. This paper applies the minimum norm method for direction of arrival estimation. Comparison of the root mean squared errors and probabilities of resolution of the minimum norm method with MUSIC for a given linear coprime or nested array demonstrates the superiority of the minimum norm method. Specifically, minimum norm method exhibits lower mean squared error, narrower peaks at the locations of the true sources, and a lower noise floor in the spatial spectral estimate. This work also formulates two different minimum norm methods for planar sparse arrays: direct and linear. Comparison of the linear minimum norm method with the linear MUSIC for planar arrays also demonstrates higher accuracy of the minimum norm method.

Product Processing for Tapered Sparse Arrays

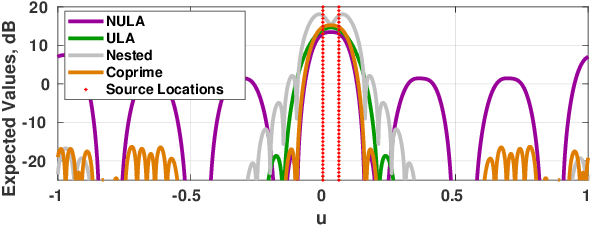
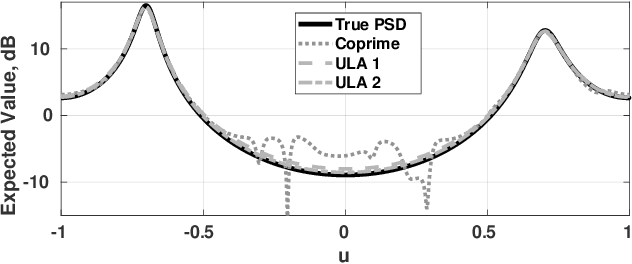
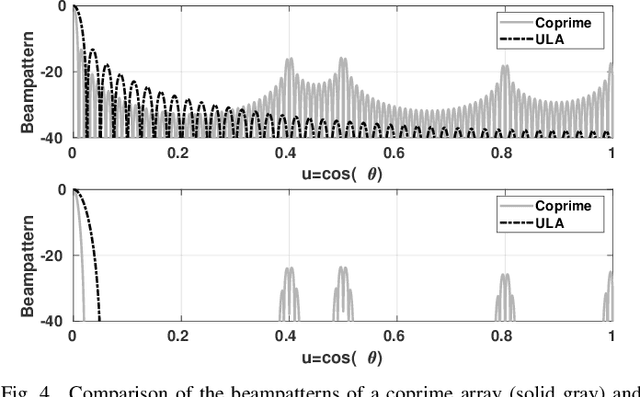
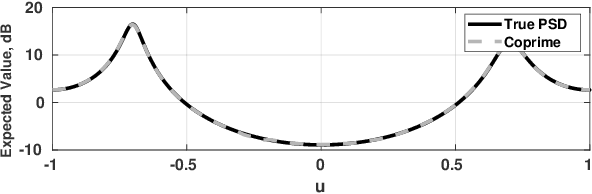
The product processor output has recently been introduced as a spatial power spectral density estimate, unifying product arrays such as coprime arrays, nested arrays, and standard uniform line arrays. The expected value and covariance function of this estimate for a white Gaussian process was derived in previous work over these various array configurations. However, this prior work used a uniform taper in all cases. In this paper, we show that when product arrays are windowed with non-uniform tapers, the expected value of the product processor output is the convolution of the true spatial power spectral density with the spatial Fourier transform of the difference coarray. This expected value makes a Fourier transform pair with a spatial autocorrelation estimate obtained by windowing the true autocorrelation function. We also derive the covariance function of the product processor output with non-uniform tapers, and compare these derived statistics for the aforementioned array geometries. Also, in prior work, the moments were provided only for linear arrays; this paper extends the estimation results to multidimensional arrays.

Absolute Eigenvalues-Based Covariance Matrix Estimation for a Sparse Array

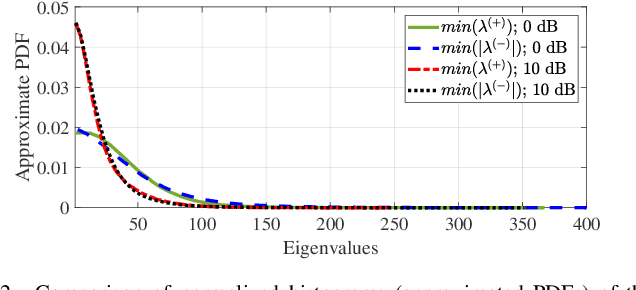
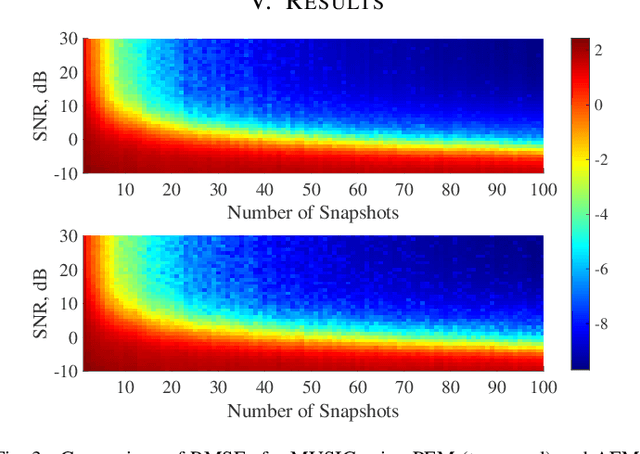
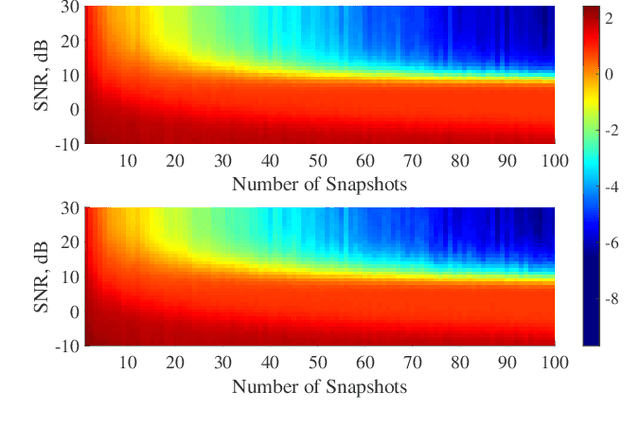
The ensemble covariance matrix of a wide sense stationary signal spatially sampled by a full linear array is positive semi-definite and Toeplitz. However, the direct augmented covariance matrix of an augmentable sparse array is Toeplitz but not positive semi-definite, resulting in negative eigenvalues that pose inherent challenges in its applications, including model order estimation and source localization. The positive eigenvalues-based covariance matrix for augmentable sparse arrays is robust but the matrix is unobtainable when all noise eigenvalues of the direct augmented matrix are negative, which is a possible case. To address this problem, we propose a robust covariance matrix for augmentable sparse arrays that leverages both positive and negative noise eigenvalues. The proposed covariance matrix estimate can be used in conjunction with subspace based algorithms and adaptive beamformers to yield accurate signal direction estimates.

Matched Illumination Waveforms using Multi-Tone Sinusoidal Frequency Modulation

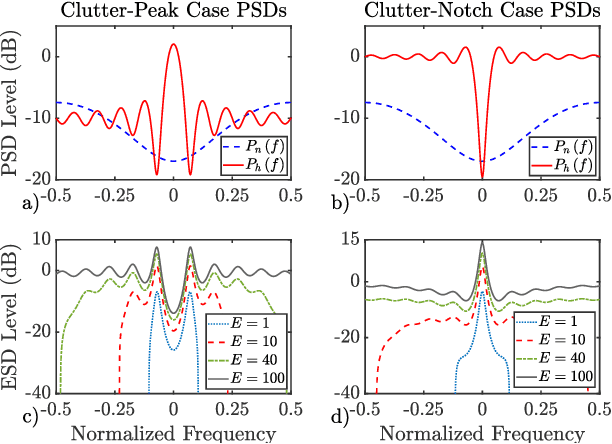
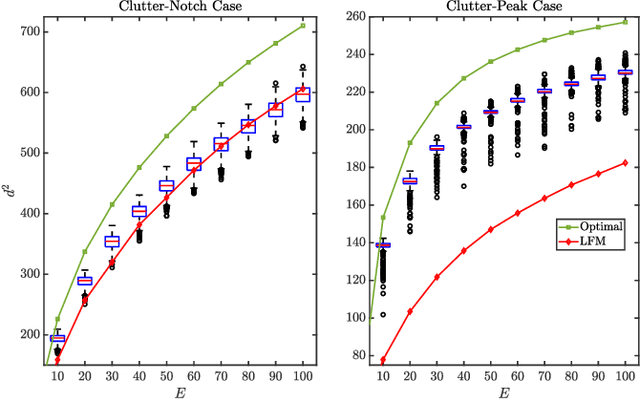
This paper explores the design of constant modulus Matched-Illumination (MI) waveforms using the Multi-Tone Sinusoidal Frequency Modulation (MTSFM) waveform model. MI waveforms are optimized for detecting targets in known noise and clutter Power Spectral Densities (PSDs). There exist well-defined information theoretic methods that describe the design of MI waveforms for a myriad of target/noise/clutter models. However, these methods generally only produce the magnitude square of the MI waveform's spectrum. Additionally, the waveform's time-series is not guaranteed to be constant modulus. The MTSFM is a constant modulus waveform model with a discrete set of design coefficients. The coefficients are adjusted to synthesize constant modulus waveforms that approximate the ideal MI waveform's spectrum. Simulations demonstrate that the MTSFM's detection performance closely approximates an ideal MI waveform spectrum and generally outperforms flat spectrum waveforms across a range of transmit energies when the noise and clutter PSDs vary greatly across the operational band.