Daniel Sartori
Product Processing for Tapered Sparse Arrays
Jun 07, 2021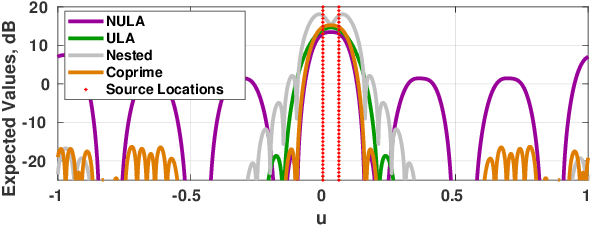
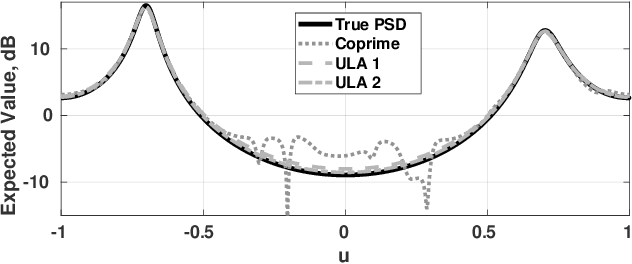
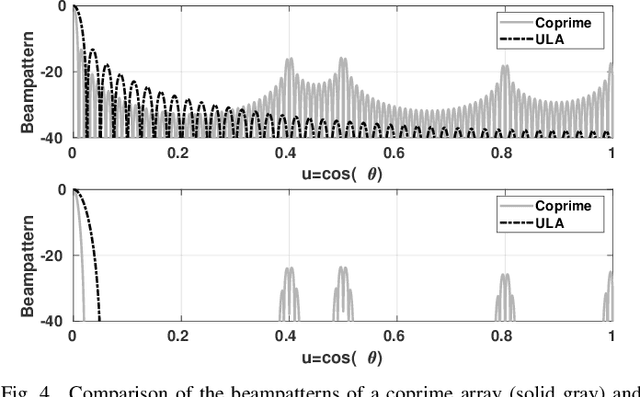
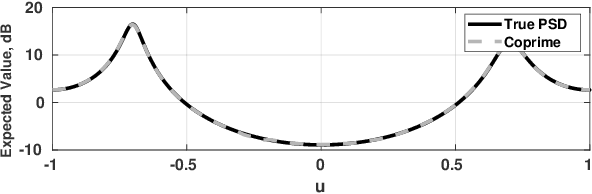
Abstract:The product processor output has recently been introduced as a spatial power spectral density estimate, unifying product arrays such as coprime arrays, nested arrays, and standard uniform line arrays. The expected value and covariance function of this estimate for a white Gaussian process was derived in previous work over these various array configurations. However, this prior work used a uniform taper in all cases. In this paper, we show that when product arrays are windowed with non-uniform tapers, the expected value of the product processor output is the convolution of the true spatial power spectral density with the spatial Fourier transform of the difference coarray. This expected value makes a Fourier transform pair with a spatial autocorrelation estimate obtained by windowing the true autocorrelation function. We also derive the covariance function of the product processor output with non-uniform tapers, and compare these derived statistics for the aforementioned array geometries. Also, in prior work, the moments were provided only for linear arrays; this paper extends the estimation results to multidimensional arrays.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge