Absolute Eigenvalues-Based Covariance Matrix Estimation for a Sparse Array
Paper and Code
Jun 07, 2021
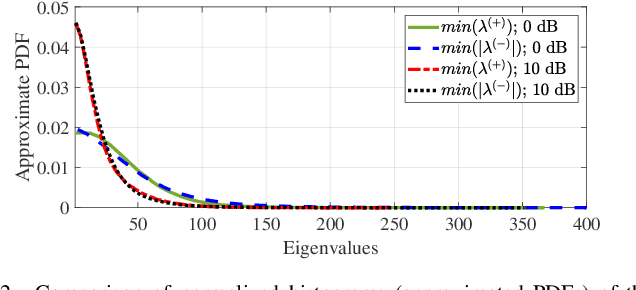
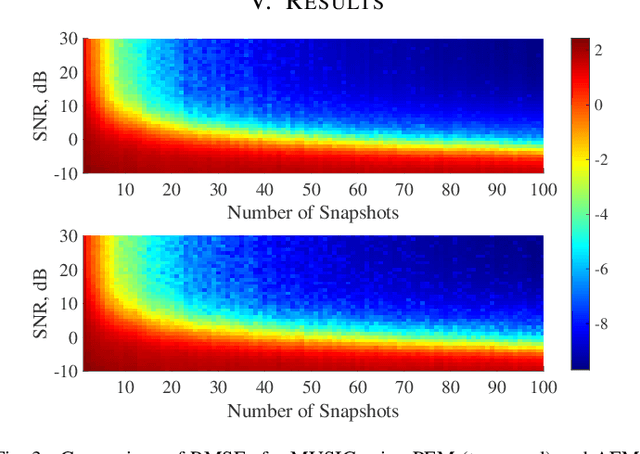
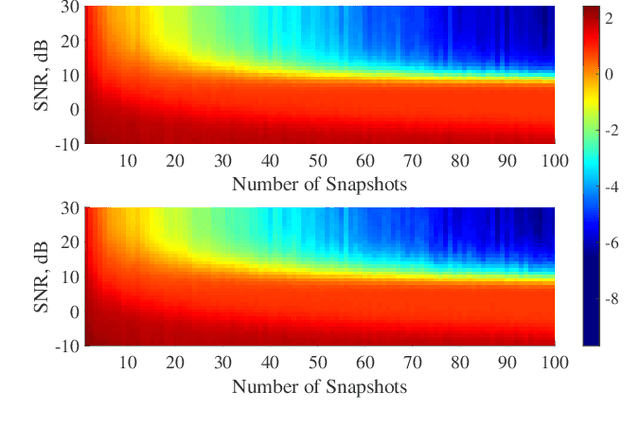
The ensemble covariance matrix of a wide sense stationary signal spatially sampled by a full linear array is positive semi-definite and Toeplitz. However, the direct augmented covariance matrix of an augmentable sparse array is Toeplitz but not positive semi-definite, resulting in negative eigenvalues that pose inherent challenges in its applications, including model order estimation and source localization. The positive eigenvalues-based covariance matrix for augmentable sparse arrays is robust but the matrix is unobtainable when all noise eigenvalues of the direct augmented matrix are negative, which is a possible case. To address this problem, we propose a robust covariance matrix for augmentable sparse arrays that leverages both positive and negative noise eigenvalues. The proposed covariance matrix estimate can be used in conjunction with subspace based algorithms and adaptive beamformers to yield accurate signal direction estimates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge