How Random is Random? Evaluating the Randomness and Humaness of LLMs' Coin Flips

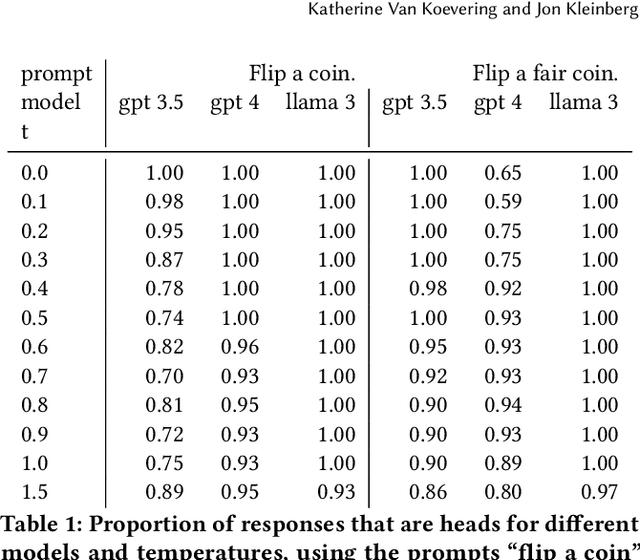
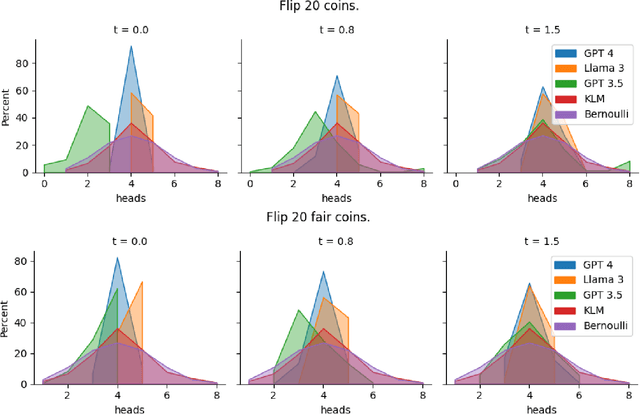
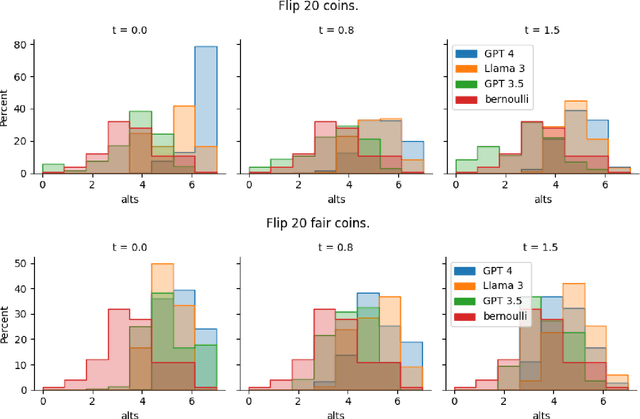
One uniquely human trait is our inability to be random. We see and produce patterns where there should not be any and we do so in a predictable way. LLMs are supplied with human data and prone to human biases. In this work, we explore how LLMs approach randomness and where and how they fail through the lens of the well studied phenomena of generating binary random sequences. We find that GPT 4 and Llama 3 exhibit and exacerbate nearly every human bias we test in this context, but GPT 3.5 exhibits more random behavior. This dichotomy of randomness or humaness is proposed as a fundamental question of LLMs and that either behavior may be useful in different circumstances.

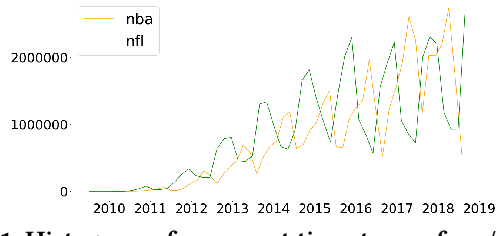
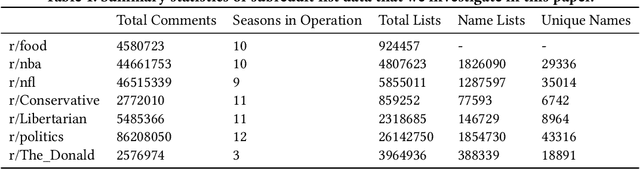
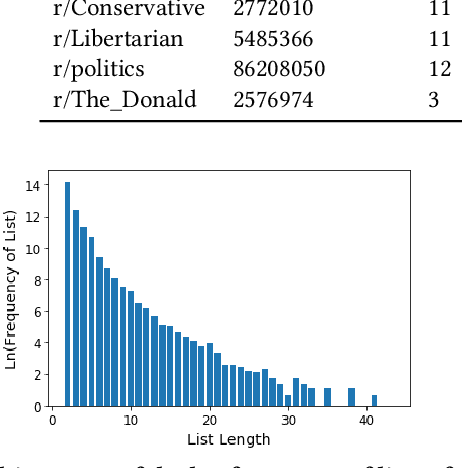
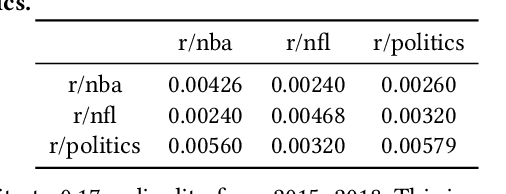
Frozen Binomials on the Web: Word Ordering and Language Conventions in Online Text

There is inherent information captured in the order in which we write words in a list. The orderings of binomials --- lists of two words separated by `and' or `or' --- has been studied for more than a century. These binomials are common across many areas of speech, in both formal and informal text. In the last century, numerous explanations have been given to describe what order people use for these binomials, from differences in semantics to differences in phonology. These rules describe primarily `frozen' binomials that exist in exactly one ordering and have lacked large-scale trials to determine efficacy. Online text provides a unique opportunity to study these lists in the context of informal text at a very large scale. In this work, we expand the view of binomials to include a large-scale analysis of both frozen and non-frozen binomials in a quantitative way. Using this data, we then demonstrate that most previously proposed rules are ineffective at predicting binomial ordering. By tracking the order of these binomials across time and communities we are able to establish additional, unexplored dimensions central to these predictions. Expanding beyond the question of individual binomials, we also explore the global structure of binomials in various communities, establishing a new model for these lists and analyzing this structure for non-frozen and frozen binomials. Additionally, novel analysis of trinomials --- lists of length three --- suggests that none of the binomials analysis applies in these cases. Finally, we demonstrate how large data sets gleaned from the web can be used in conjunction with older theories to expand and improve on old questions.