Prognostics and Health Management of Wafer Chemical-Mechanical Polishing System using Autoencoder

The Prognostics and Health Management Data Challenge (PHM) 2016 tracks the health state of components of a semiconductor wafer polishing process. The ultimate goal is to develop an ability to predict the measurement on the wafer surface wear through monitoring the components health state. This translates to cost saving in large scale production. The PHM dataset contains many time series measurements not utilized by traditional physics based approach. On the other hand task, applying a data driven approach such as deep learning to the PHM dataset is non-trivial. The main issue with supervised deep learning is that class label is not available to the PHM dataset. Second, the feature space trained by an unsupervised deep learner is not specifically targeted at the predictive ability or regression. In this work, we propose using the autoencoder based clustering whereby the feature space trained is found to be more suitable for performing regression. This is due to having a more compact distribution of samples respective to their nearest cluster means. We justify our claims by comparing the performance of our proposed method on the PHM dataset with several baselines such as the autoencoder as well as state-of-the-art approaches.

Deep Clustering using Dirichlet Process Gaussian Mixture and Alpha Jensen-Shannon Divergence Clustering Loss

Deep clustering is an emerging topic in deep learning where traditional clustering is performed in deep learning feature space. However, clustering and deep learning are often mutually exclusive. In the autoencoder based deep clustering, the challenge is how to jointly optimize both clustering and dimension reduction together, so that the weights in the hidden layers are not only guided by reconstruction loss, but also by a loss function associated with clustering. The current state-of-the-art has two fundamental flaws. First, they rely on the mathematical convenience of Kullback-Leibler divergence for the clustering loss function but the former is asymmetric. Secondly, they assume the prior knowledge on the number of clusters is always available for their dataset of interest. This paper tries to improve on these problems. In the first problem, we use a Jensen-Shannon divergence to overcome the asymmetric issue, specifically using a closed form variant. Next, we introduce an infinite cluster representation using Dirichlet process Gaussian mixture model for joint clustering and model selection in the latent space which we called deep model selection. The number of clusters in the latent space are not fixed but instead vary accordingly as they gradually approach the optimal number during training. Thus, prior knowledge is not required. We evaluate our proposed deep model selection method with traditional model selection on large class number datasets such as MIT67 and CIFAR100 and also compare with both traditional variational Bayes model and deep clustering method with convincing results.

Deep clustering using adversarial net based clustering loss

Deep clustering is a recent deep learning technique which combines deep learning with traditional unsupervised clustering. At the heart of deep clustering is a loss function which penalizes samples for being an outlier from their ground truth cluster centers in the latent space. The probabilistic variant of deep clustering reformulates the loss using KL divergence. Often, the main constraint of deep clustering is the necessity of a closed form loss function to make backpropagation tractable. Inspired by deep clustering and adversarial net, we reformulate deep clustering as an adversarial net over traditional closed form KL divergence. Training deep clustering becomes a task of minimizing the encoder and maximizing the discriminator. At optimality, this method theoretically approaches the JS divergence between the distribution assumption of the encoder and the discriminator. We demonstrated the performance of our proposed method on several well cited datasets such as SVHN, USPS, MNIST and CIFAR10, achieving on-par or better performance with some of the state-of-the-art deep clustering methods.

Stochastic Learning of Non-Conjugate Variational Posterior for Image Classification

Large scale Bayesian nonparametrics (BNP) learner such as stochastic variational inference (SVI) can handle datasets with large class number and large training size at fractional cost. Like its predecessor, SVI rely on the assumption of conjugate variational posterior to approximate the true posterior. A more challenging problem is to consider large scale learning on non-conjugate posterior. Recent works in this direction are mostly associated with using Monte Carlo methods for approximating the learner. However, these works are usually demonstrated on non-BNP related task and less complex models such as logistic regression, due to higher computational complexity. In order to overcome the issue faced by SVI, we develop a novel approach based on the recently proposed variational maximization-maximization (VMM) learner to allow large scale learning on non-conjugate posterior. Unlike SVI, our VMM learner does not require closed-form expression for the variational posterior expectatations. Our only requirement is that the variational posterior is differentiable. In order to ensure convergence in stochastic settings, SVI rely on decaying step-sizes to slow its learning. Inspired by SVI and Adam, we propose the novel use of decaying step-sizes on both gradient and ascent direction in our VMM to significantly improve its learning. We show that our proposed methods is compatible with ResNet features when applied to large class number datasets such as MIT67 and SUN397. Finally, we compare our proposed learner with several recent works such as deep clustering algorithms and showed we were able to produce on par or outperform the state-of-the-art methods in terms of clustering measures.

Boundary-Decoder network for inverse prediction of capacitor electrostatic analysis

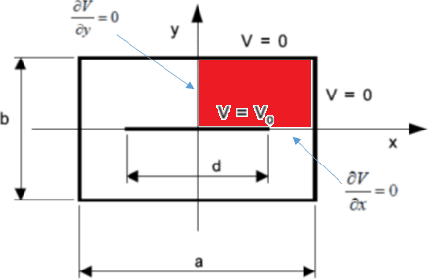
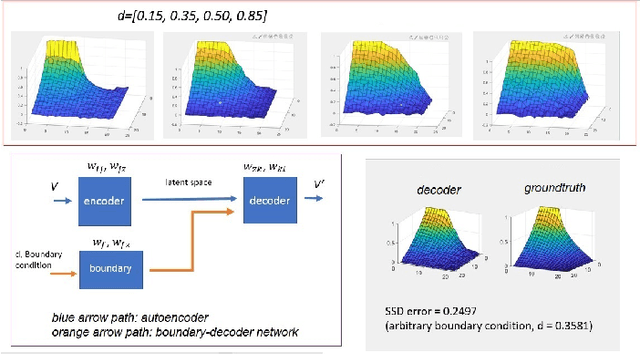
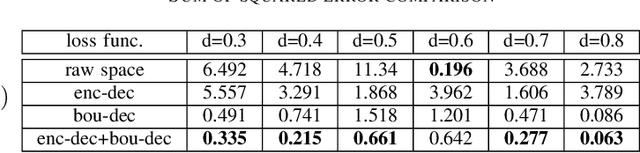
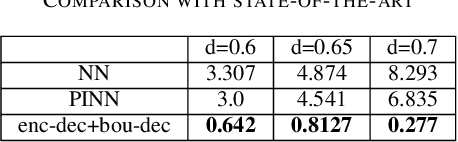
Traditional electrostatic simulation are meshed-based methods which convert partial differential equations into an algebraic system of equations and their solutions are approximated through numerical methods. These methods are time consuming and any changes in their initial or boundary conditions will require solving the numerical problem again. Newer computational methods such as the physics informed neural net (PINN) similarly require re-training when boundary conditions changes. In this work, we propose an end-to-end deep learning approach to model parameter changes to the boundary conditions. The proposed method is demonstrated on the test problem of a long air-filled capacitor structure. The proposed approach is compared to plain vanilla deep learning (NN) and PINN. It is shown that our method can significantly outperform both NN and PINN under dynamic boundary condition as well as retaining its full capability as a forward model.