Forecasting Multilinear Data via Transform-Based Tensor Autoregression

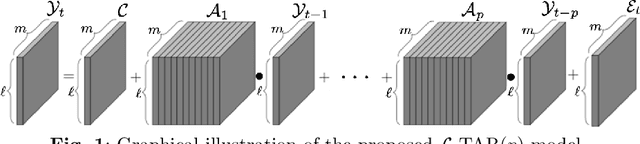
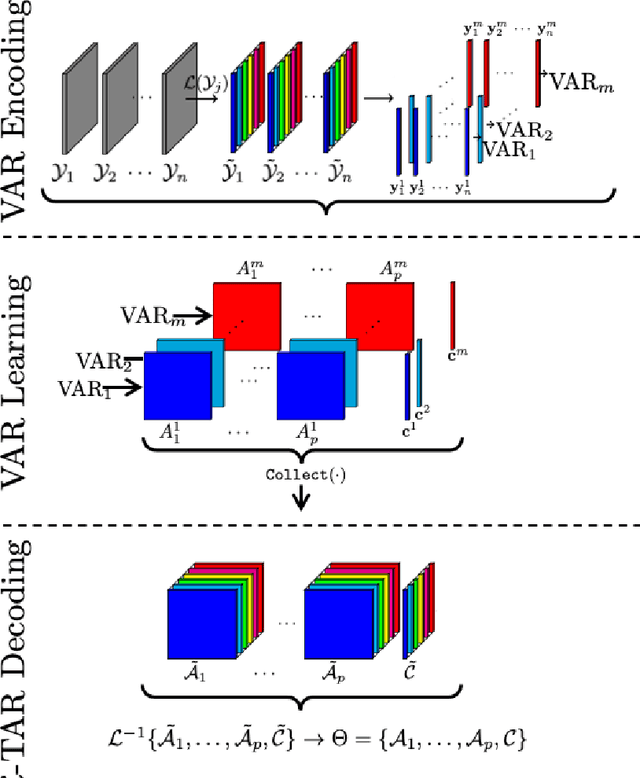
In the era of big data, there is an increasing demand for new methods for analyzing and forecasting 2-dimensional data. The current research aims to accomplish these goals through the combination of time-series modeling and multilinear algebraic systems. We expand previous autoregressive techniques to forecast multilinear data, aptly named the L-Transform Tensor autoregressive (L-TAR for short). Tensor decompositions and multilinear tensor products have allowed for this approach to be a feasible method of forecasting. We achieve statistical independence between the columns of the observations through invertible discrete linear transforms, enabling a divide and conquer approach. We present an experimental validation of the proposed methods on datasets containing image collections, video sequences, sea surface temperature measurements, stock prices, and networks.

High-Order Multilinear Discriminant Analysis via Order-$\textit{n}$ Tensor Eigendecomposition

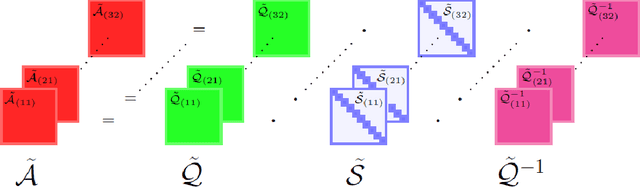
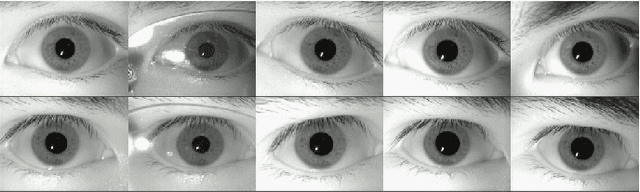
Higher-order data with high dimensionality is of immense importance in many areas of machine learning, computer vision, and video analytics. Multidimensional arrays (commonly referred to as tensors) are used for arranging higher-order data structures while keeping the natural representation of the data samples. In the past decade, great efforts have been made to extend the classic linear discriminant analysis for higher-order data classification generally referred to as multilinear discriminant analysis (MDA). Most of the existing approaches are based on the Tucker decomposition and $\textit{n}$-mode tensor-matrix products. The current paper presents a new approach to tensor-based multilinear discriminant analysis referred to as High-Order Multilinear Discriminant Analysis (HOMLDA). This approach is based upon the tensor decomposition where an order-$\textit{n}$ tensor can be written as a product of order-$\textit{n}$ tensors and has a natural extension to traditional linear discriminant analysis (LDA). Furthermore, the resulting framework, HOMLDA, might produce a within-class scatter tensor that is close to singular. Thus, computing the inverse inaccurately may distort the discriminant analysis. To address this problem, an improved method referred to as Robust High-Order Multilinear Discriminant Analysis (RHOMLDA) is introduced. Experimental results on multiple data sets illustrate that our proposed approach provides improved classification performance with respect to the current Tucker decomposition-based supervised learning methods.

A New Approach to Multilinear Dynamical Systems and Control

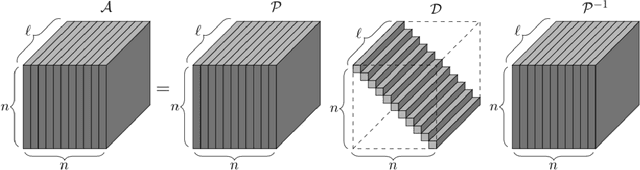
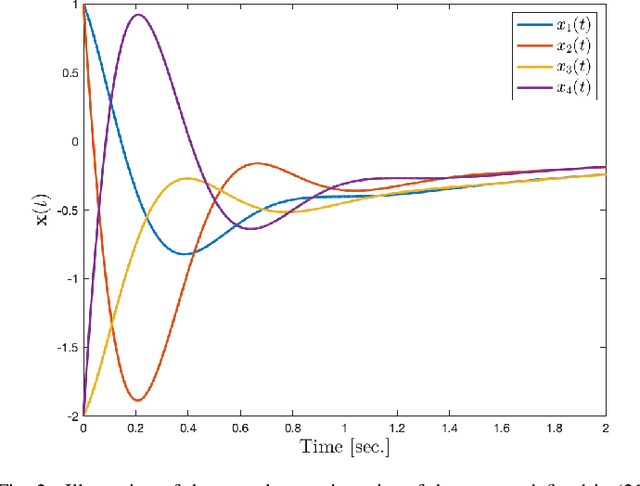
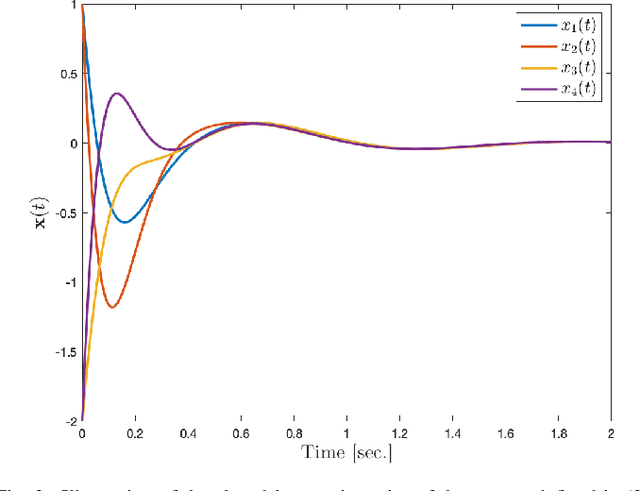
The current paper presents a new approach to multilinear dynamical systems analysis and control. The approach is based upon recent developments in tensor decompositions and a newly defined algebra of circulants. In particular, it is shown that under the right tensor multiplication operator, a third order tensor can be written as a product of third order tensors that is analogous to a traditional matrix eigenvalue decomposition where the "eigenvectors" become eigenmatrices and the "eigenvalues" become eigen-tuples. This new development allows for a proper tensor eigenvalue decomposition to be defined and has natural extension to linear systems theory through a \textit{tensor-exponential}. Through this framework we extend many of traditional techniques used in linear system theory to their multilinear counterpart.