A New Approach to Multilinear Dynamical Systems and Control
Paper and Code
Aug 31, 2021
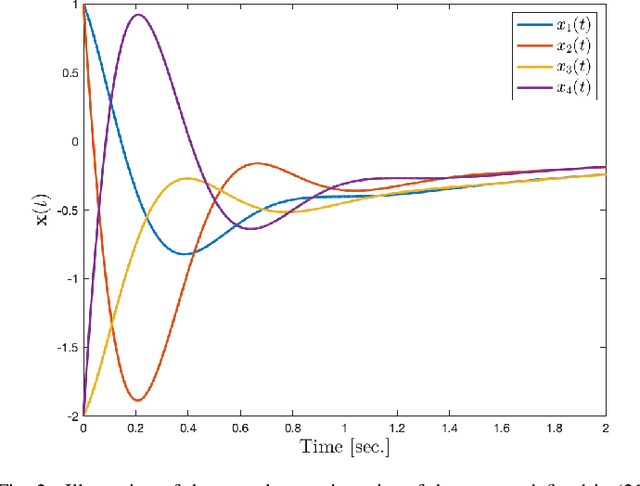
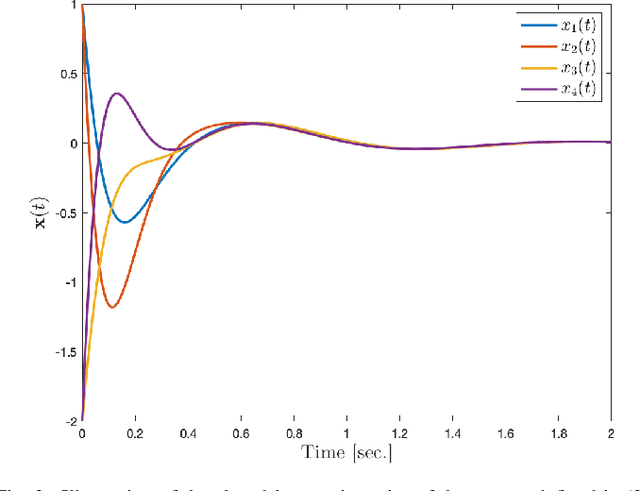
The current paper presents a new approach to multilinear dynamical systems analysis and control. The approach is based upon recent developments in tensor decompositions and a newly defined algebra of circulants. In particular, it is shown that under the right tensor multiplication operator, a third order tensor can be written as a product of third order tensors that is analogous to a traditional matrix eigenvalue decomposition where the "eigenvectors" become eigenmatrices and the "eigenvalues" become eigen-tuples. This new development allows for a proper tensor eigenvalue decomposition to be defined and has natural extension to linear systems theory through a \textit{tensor-exponential}. Through this framework we extend many of traditional techniques used in linear system theory to their multilinear counterpart.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge