Joint Resource-Power Allocation and UE Rank Selection in Multi-User MIMO Systems with Linear Transceivers

Next-generation wireless networks aim to deliver data speeds much faster than 5G. This requires base stations with lots of antennas and a large operating bandwidth. These advanced base stations are expected to serve several multi-antenna user-equipment (UEs) simultaneously on the same time-frequency resources on both the uplink and the downlink. The UE data rates are affected by the following three main factors: UE rank, which refers to the number of data layers used by each UE, UE frequency allocation, which refers to the assignment of slices of the overall frequency band to use for each UE in an orthogonal frequency-division multiplexing (OFDM) system, and UE power allocation/control, which refers to the power allocated by the base station for data transmission to each UE on the downlink or the power used by the UE to send data on the uplink. Since multiple UEs are to be simultaneously served, the type of precoder used for downlink transmission and the type of receiver used for uplink reception predominantly influence these three aforementioned factors and the resulting overall UE throughput. This paper addresses the problem of jointly selecting these three parameters specifically when zero-forcing (ZF) precoders are used for downlink transmission and linear minimum mean square error (LMMSE) receivers are employed for uplink reception.

Attacking and Defending Deep-Learning-Based Off-Device Wireless Positioning Systems

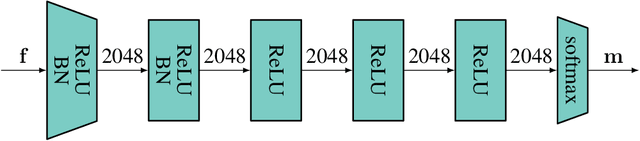
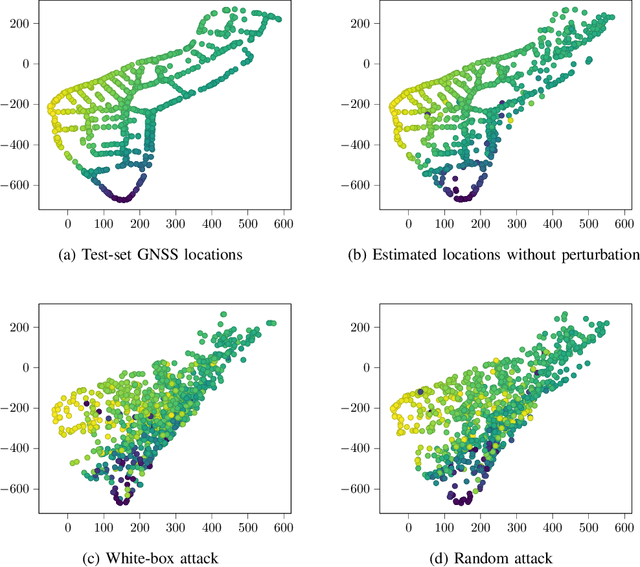
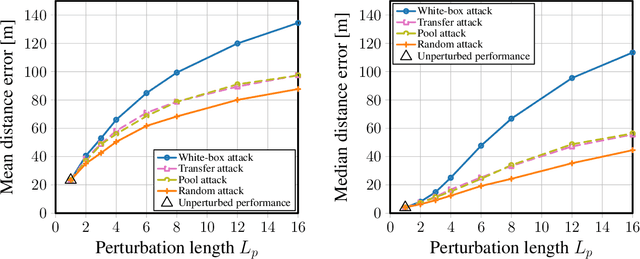
Localization services for wireless devices play an increasingly important role and a plethora of emerging services and applications already rely on precise position information. Widely used on-device positioning methods, such as the global positioning system, enable accurate outdoor positioning and provide the users with full control over what services are allowed to access location information. To provide accurate positioning indoors or in cluttered urban scenarios without line-of-sight satellite connectivity, powerful off-device positioning systems, which process channel state information (CSI) with deep neural networks, have emerged recently. Such off-device positioning systems inherently link a user's data transmission with its localization, since accurate CSI measurements are necessary for reliable wireless communication -- this not only prevents the users from controlling who can access this information but also enables virtually everyone in the device's range to estimate its location, resulting in serious privacy and security concerns. We propose on-device attacks against off-device wireless positioning systems in multi-antenna orthogonal frequency-division multiplexing systems while minimizing the impact on quality-of-service, and we demonstrate their efficacy using measured datasets for outdoor and indoor scenarios. We also investigate defenses to counter such attack mechanisms, and we discuss the limitations and implications on protecting location privacy in future wireless communication systems.

Bit-Metric Decoding Rate in Multi-User MIMO Systems: Theory

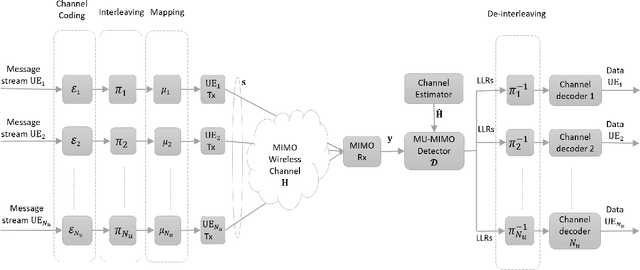
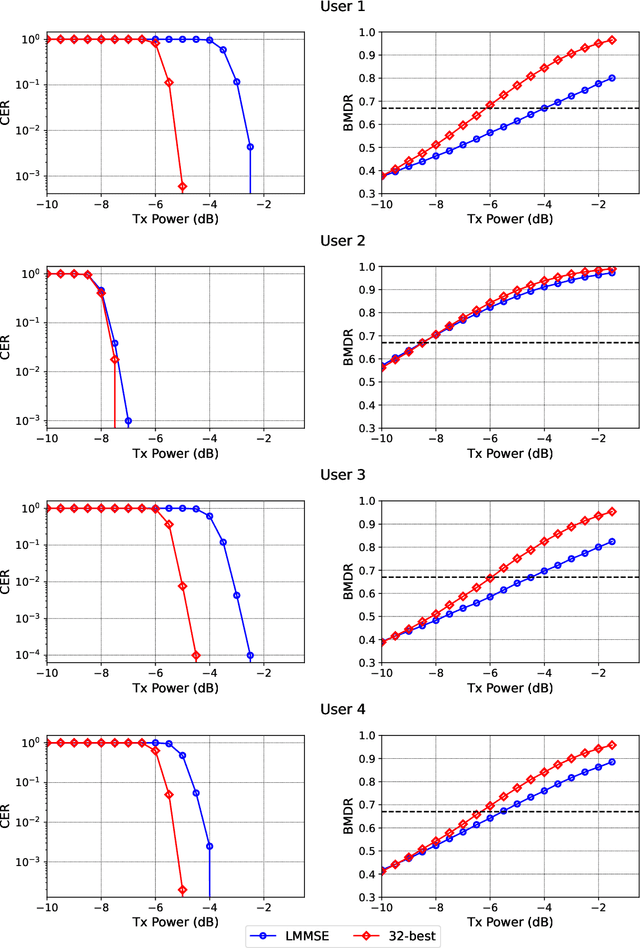
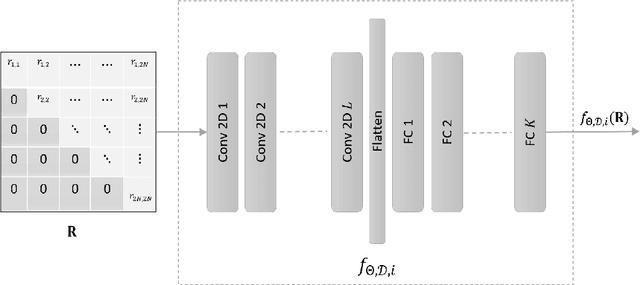
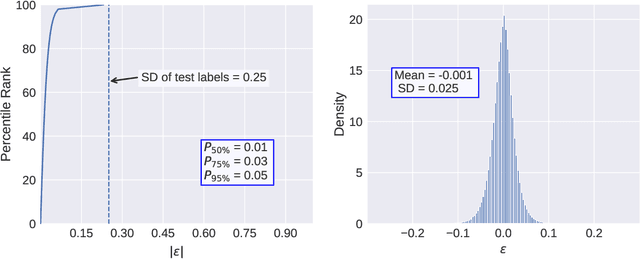
Link-adaptation (LA) is one of the most important aspects of wireless communications where the modulation and coding scheme (MCS) used by the transmitter is adapted to the channel conditions in order to meet a certain target error-rate. In a single-user SISO (SU-SISO) system, LA is performed by computing the post-equalization signal-to-interference-noise ratio (SINR) at the receiver. The same technique can be employed in multi-user MIMO (MU-MIMO) receivers that use linear detectors. Another important use of post-equalization SINR is for physical layer (PHY) abstraction, where several PHY blocks like the channel encoder, the detector, and the channel decoder are replaced by an abstraction model in order to speed up system-level simulations. This is achieved by mapping the post-equalization SINR to a codeword error rate (CER) or a block error rate (BLER). However, for MU-MIMO systems with non-linear receivers, like those that use variants of the sphere-decoder algorithm, there is no known equivalent of post-equalization SINR which makes both LA and PHY abstraction extremely challenging. This important issue is addressed in this two-part paper. A metric called the bit-metric decoding rate (BMDR) of a detector for a set of channel realizations is presented in this part. BMDR is the proposed equivalent of post-equalization SINR for arbitrary detectors. Since BMDR does not have a closed form expression that would enable its instantaneous calculation, a machine-learning approach to predict it is presented. The second part describes the algorithms to perform LA, detector selection, and PHY abstraction using BMDR for MU-MIMO systems with arbitrary detectors. Extensive simulation results corroborating the claims are presented.

Bit-Metric Decoding Rate in Multi-User MIMO Systems: Applications

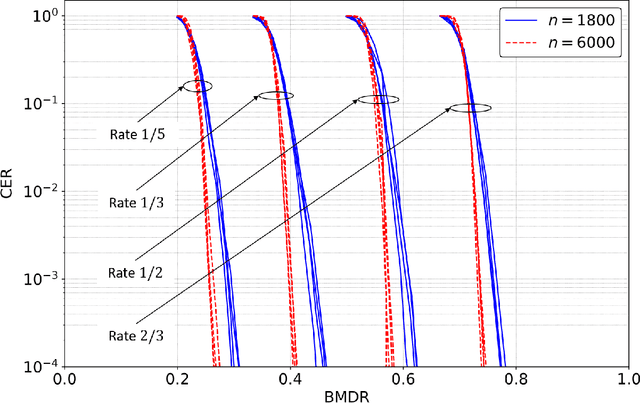
This is the second part of a two-part paper that focuses on link-adaptation (LA) and physical layer (PHY) abstraction for multi-user MIMO (MU-MIMO) systems with non-linear receivers. The first part proposes a new metric, called bit-metric decoding rate (BMDR) for a detector, as being the equivalent of post-equalization signal-to-interference-noise ratio (SINR) for non-linear receivers. Since this BMDR does not have a closed form expression, a machine-learning based approach to estimate it effectively is presented. In this part, the concepts developed in the first part are utilized to develop novel algorithms for LA, dynamic detector selection from a list of available detectors, and PHY abstraction in MU-MIMO systems with arbitrary receivers. Extensive simulation results that substantiate the efficacy of the proposed algorithms are presented.

Cluster-Seeking James-Stein Estimators

This paper considers the problem of estimating a high-dimensional vector of parameters $\boldsymbol{\theta} \in \mathbb{R}^n$ from a noisy observation. The noise vector is i.i.d. Gaussian with known variance. For a squared-error loss function, the James-Stein (JS) estimator is known to dominate the simple maximum-likelihood (ML) estimator when the dimension $n$ exceeds two. The JS-estimator shrinks the observed vector towards the origin, and the risk reduction over the ML-estimator is greatest for $\boldsymbol{\theta}$ that lie close to the origin. JS-estimators can be generalized to shrink the data towards any target subspace. Such estimators also dominate the ML-estimator, but the risk reduction is significant only when $\boldsymbol{\theta}$ lies close to the subspace. This leads to the question: in the absence of prior information about $\boldsymbol{\theta}$, how do we design estimators that give significant risk reduction over the ML-estimator for a wide range of $\boldsymbol{\theta}$? In this paper, we propose shrinkage estimators that attempt to infer the structure of $\boldsymbol{\theta}$ from the observed data in order to construct a good attracting subspace. In particular, the components of the observed vector are separated into clusters, and the elements in each cluster shrunk towards a common attractor. The number of clusters and the attractor for each cluster are determined from the observed vector. We provide concentration results for the squared-error loss and convergence results for the risk of the proposed estimators. The results show that the estimators give significant risk reduction over the ML-estimator for a wide range of $\boldsymbol{\theta}$, particularly for large $n$. Simulation results are provided to support the theoretical claims.